Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.6. Explore 2

Mathematics 20-3 Module 6

Module 6: Surface Area

 

Self-Check 1

 

This is a photo of hailstones in green grass.

Hemera/Thinkstock

Hailstones gather additional ice on their surfaces as violent updrafts in storm clouds carry them upwards to elevations where the temperature is below freezing. The hailstone circled in red in the photograph is approximately 6 mm in diameter. What is its surface area? Round to the nearest 10 mm2. Answer

 

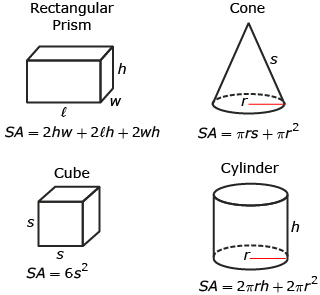
In previous mathematics courses, you explored several formulas for surface area. These formulas included the surface areas of cubes, rectangular prisms, cones, and cylinders. The following chart summarizes these formulas. You may find these formulas helpful for the following problems.

 

This is an illustration of area formulas.

This is a photo of an individual working with sheet metal .

Hemera/Thinkstock

Air vents, climate-control ducts, roofing, siding for houses, machinery, traffic and warning signs, car bumpers, railway cars, manufacturing equipment, and many other items use sheet metal. Workers are given a certain surface area and may be asked to determine maximum dimensions with an allotted amount of sheet metal.

 

Manipulating surface area formulas is a useful concept for sheet-metal workers.

 

Try This 2

 

Ross, a sheet-metal worker, makes a closed rectangular duct that is 32 in long, 15 in wide, and 16 in high, as shown.

 

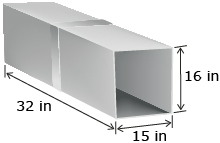
This is an image of a metal duct with a length of 32 inches, a width of 15 inches, and a height of 16 inches.

  1. Draw a net of the duct. How many sides does the net have? hint

  2. Calculate the area of each side in the net. hint

  3. Since there are no ends to the duct, how would you change the formula for the surface area of a rectangular prism to find the surface area for this duct? hint

  4. Ross has the same amount of metal as you calculated in question 2. He is to make a duct that is also 32 in long, but that has a width of 8 in. Sketch a net of the duct Ross is to fabricate.

  5. Calculate the height of the new duct. hint hint

course folder Save all your work and calculations from Try This 2 in your course folder.

 

The new height will be 23 in.
Solve for h in the surface area formula you made in question 3.
Since there are no ends to the duct, the “2wh” term is removed from the formula.
Did you get a total area of 1984 in2?
There should be four sides in the net for the duct.