Lesson 3

In the next example, you will see one way that the formula for surface area of a sphere can be manipulated. Even though the formula has r2 in it, you can find a value for the variable r.

 

Example

 

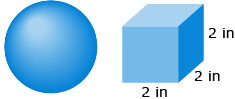
A cube is 2 in on each side. To the nearest tenth of an inch, what is the diameter of a sphere with the same surface area?

 

 

Solution

 

First, determine the surface area of the cube.   Each side of the cube (s) is 2 in.
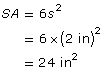Since the sphere has the same surface area as the cube, substitute the 24 in2 into the surface area formula for a sphere.
The question asks for the diameter of the sphere.   The diameter is twice the radius.   Therefore, the diameter of the sphere is about 2.8 in.	2 × 1.4 in = 2.8 in

 

Example

 

Dowels are small, cylindrical pieces of wood that fit into holes at the joint of two larger pieces of wood to add stability to the joint. Using dowels to fasten wood works well in making shelves, cabinets, and small pieces of wooden furniture.

1. A cylindrical dowel is 0.25 inches in diameter and its length is 1 in. To keep the dowel in place, glue is spread over its entire surface. What is the surface area of each dowel, to the nearest hundredth of an inch?

2. How long would a dowel with the same diameter be if its surface area was exactly 2 in2? Round your answer to the nearest hundredth of an inch.

Solution

 

Click the button on the left to watch the “Cylindrical Dowel Solution” to see a possible way to solve this problem.