Lesson 4

Explore

 

In Discover you examined the relationship between the linear scale factor (the number by which each dimension is multiplied) and the surface area scale factor of a cube.

 

You may have noticed that the surface area changed by a scale factor equal to the linear scale factor squared. The following equation summarizes this relationship:

 

area scale factor = (linear scale factor)2

 

So, for example, if you multiplied each of the dimensions of a cube by a factor of 5, the area of the new cube would be 52, or 25, times larger than the original prism.

 

Does this relationship apply to all three-dimensional objects? You will investigate this question in Try This 2.

 

Try This 2

1.  Step 1: Click on the button to open the Exploring Surface Area, Volume, and Nets—Explore It applet.
   
   
   
   

   Step 2: On both the left and right sides of the screen, choose the rectangular prism from the list of objects and make sure you've got “Surface Area” selected. Set the dimensions on the left and right sides as indicated in the following chart. Determine the surface area scale factor for the rectangular prism the same way you did in Try This 1. Record the surface area scale factor in a chart like the one shown below.
   
   

   Step 3: Repeat Step 2 for each 3-D object listed in the chart. Record the surface area scale factor for each object.
   
   

   Object	Left Dimensions	Right Dimensions	Linear Scale Factor	Surface Area Scale Factor
   Rectangular Prism	2 m × 2 m × 2 m	6 m × 6 m × 6 m	3
   Rectangular Pyramid	5 m × 5 m × 5 m	10 m × 10 m × 10 m	2
   Triangular Prism	2 m × 2 m	6 m × 6 m	3
   Cylinder	2 m × 2 m	8 m × 8 m	4
   Cone	5 m × 5 m	10 m × 10 m	2

2. Blowing bubbles is a favourite pastime for children of all ages. One bubble has a diameter of 2 cm. A second bubble has a diameter of 6 cm.
   
   
   Lifesize/Thinkstock
   
   
   1. Use the formula 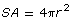to calculate the surface area of each bubble. Round to the nearest tenth.
      
      surface area of small bubble =
      
      surface area of large bubble =
      
      
   2. Compare the surface area of the large bubble to the surface area of the small bubble. What do you notice?
      
      
   3. What linear scale factor is applied to the small bubble to get the large bubble?
      
      
   4. What surface area scale factor is applied to the small bubble to get the large bubble?

Save your responses in your course folder.

 

Share 2

 

Share your responses to the questions in Try This 2 with a classmate or with a group of people. Discuss the following question:

• How did your observations of prisms, pyramids, cylinders, cones, and spheres compare with your observations of the cube in Discover? Did you see a similar relationship between the linear scale factor and the surface area scale factor?

If required, save a copy of your discussion in your course folder.