Lesson 4

Work through the following example.

 

Example

1. How many times more icing would be needed for a wedding cake if it were made 1.5 times larger in diameter and 1.5 times higher? Assume the icing would be the same thickness.

2. If you just wanted to double the icing, how many times larger in diameter and height would you have to make the larger cake? Round your answer to one decimal place.

Solution

1. The scale of the larger cake = 1.5 × the smaller cake
   
   Linear scale factor = 1.5
   
   
    
   
   
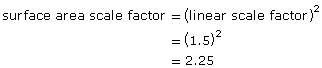
   To ice the larger cake, you would need 2.25 times as much icing as you would to ice the smaller cake.
   
   
2. 
   
   To double the amount of icing, the larger cake would be about 1.4 times larger than the smaller cake in height and diameter.

Self-Check 1

1. Two cones are similar in shape. The small cone has a radius of 10 cm and a height of 8 cm. The large cone is 16 times larger in surface area than the small cone. What is the radius and height of the large cone? Answer
   
   
2. The amount of material used to make the small teddy bear is 2 ft2. The amount of material used to make the identical looking, but larger, teddy bear is 6 ft2. What is the linear scale factor? Round to one decimal place.
   
   
   Polka Dot/Thinkstock
   
   Answer
   
   
3. A model locomotive is built to 1:32 scale. How many times larger in surface area is the actual locomotive?
   
   
   iStockphoto/Thinkstock
   
   Answer
   
   

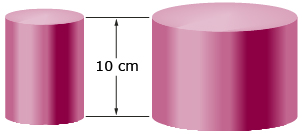
4. Natsuko is comparing open-ended cylinders. She notes that the radius of the second cylinder is double the radius of the first. She says that the surface area of the second cylinder is 22, or 4, times the surface area of the first cylinder.
   
   
   
   

   1. Find the area of each cylindrical surface. Use . Answer
      
      
   2. How much larger is the surface area of the second cylinder than the first? Answer
       
   3. Was Natsuko correct? Why or why not? Answer
      

---