Lesson 1

 

What about estimating the volume of a sphere? A unit cube wouldn’t be all that useful, so another method of estimating is needed.

 

 

Method 2: Estimating Linear Dimensions

 

A second method of estimating volume and capacity is to use estimates of the object’s linear dimensions. In this method you round known measurements to numbers that are easier to work with. Then you use the volume formula to calculate an approximate volume or capacity.

 

Example

 

Assume you used a ruler to find the linear measurements of a dresser to be 3.2 ft wide, 4.1 ft tall, and 1.9 ft deep. Estimate the volume of space the dresser occupies in the room.

 

Solution

 

Round the measurements to numbers that are easier to work with.

 

3.2 ft wide rounds to 3 ft wide

4.1 ft tall rounds to 4 ft tall

1.9 ft deep rounds to 2 ft deep

 

Since the dresser has a rectangular prism shape, use the volume formula for a rectangular prism.

 

 

Substitute in the rounded measurements.

 

 

The dresser has an estimated volume of 24 ft3.

---

In the next example you will see how this method works for different-shaped objects. The following example uses a referent, instead of a ruler, to approximate the linear dimensions. Then the estimations are put into the appropriate volume formula.

 

Example

 

Miko would like to estimate the capacity of a slush cup. She does not have a ruler and finds it difficult to visualize how many sugar cubes occupy the same space. But Miko knows the nail on her forefinger is very close to 1 cm in width. She uses this referent to measure the cup’s height and diameter. Miko’s estimates are 20 cm in height and 8 cm in diameter. What is Miko’s estimate for the capacity of the slush cup?

 

Solution

 

The diameter is 8 cm. Therefore, the radius is 4 cm. To approximate the value of pi, 3 is used.

 

Since the cup’s shape is close to a cylinder, use the volume formula for a cylinder:

 

 

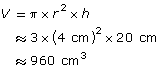
The cubic centimetre is a unit of volume. Since capacity is asked for, convert the unit to a unit of capacity.

 

Remember that 1 mL = 1 cm3; therefore, 960 cm3 = 960 mL.

 

Miko estimates the slush cup has a capacity of approximately 960 mL.

 

Self-Check 3

1. Would you use cubic inches or cubic yards as an imperial unit of measure to determine the volume of your textbook? Use a referent to estimate the volume of your textbook. Answer
   
   
2.  
   1. If you were describing the capacity of a refrigerator or freezer using the imperial system, what imperial unit would be most appropriate? Answer
      
      
   2. Estimate the capacity of the inside of your fridge or freezer using linear-dimension estimates. Answer