Lesson 3
1. Lesson 3
1.5. Explore
Module 7: Volume and Capacity
Explore
![]()
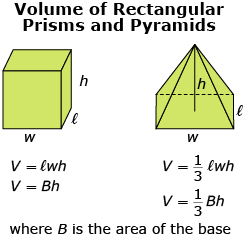
These formulas can be used to calculate the capacity of prisms and pyramids.
In Try This 1 you investigated the relationship between the volume of a rectangular prism and the volume of a pyramid with the same base, B, and height, h. You may have noticed that the volume of the pyramid is one-third the volume of the rectangular prism. This relationship can be seen in these formulas.
Example

Goodshoot/Thinkstock
Determine the volume of the Pyramid of Khafre. The base has a length of 215.5 m on each side and rises to a height of 136.4 m. Round your answer to the nearest 100 m3.
Solution
Find the area of the square base, B.
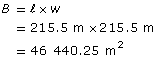
Find the volume of the pyramid. Substitute in the base, B.
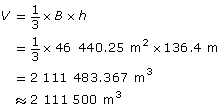
The volume of the Pyramid of Khafre is approximately 2 111 500 m3.
Self-Check 1
- A pyramid has the same base and height as a cube with 6 cm on each side. What is the volume of this pyramid?
 Answer
Answer
-
The interior of the crystal decoration in the photograph is a pyramid. The decoration is 6 cm deep.The top is a square that measures 8 cm on a side. What is the crystal’s capacity in millilitres? Round your answer to the nearest millilitre. Answer

A cube is a rectangular prism.