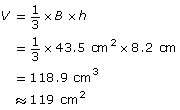Lesson 3

1. Lesson 3

1.6. Explore 2

Mathematics 20-3 Module 7

Module 7: Volume and Capacity

The Volume and Capacity of Pyramids with Regular Polygon Faces

Regardless of the shape of the base of a prism or pyramid, the formula for volume remains the same. The base can be any shape that you can find the area of.

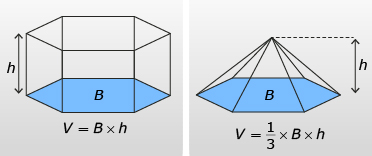
The prism and pyramid in these two graphics have the same base and height.

Example

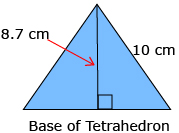
A tetrahedron is a pyramid made up of four equilateral triangles. Each side of this tetrahedron is 10 cm long.

This is a graphic of a regular tetrahedron.

The vertical height from apex to base is 8.7 cm.

This is a graphic of the base of a regular tetrahedron.

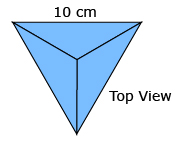
When its net is folded out, the sides of each triangle are 10 cm long.

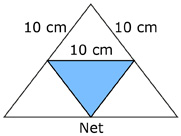
This is a graphic of the net of a regular tetrahedron.

Determine, to the nearest cubic centimetre, the volume of this tetrahedron.

Solution

First, find the area of the triangular base, B.

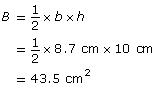
Use the formula for the volume of a pyramid. The perpendicular or vertical height, h, of the tetrahedron is 8.2 cm. The volume of the tetrahedron is approximately 119 cm3.