Lesson 3

 

Example

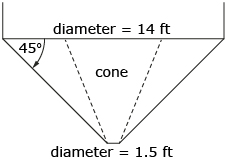
1. If the 45° conical hopper of one of these grain bins has an upper diameter of 14 ft and a diameter at the shut-off of 1.5 ft, what is the hopper’s capacity? Round your answer to the nearest cubic foot.
   
   
2. If an imperial bushel is approximately 1.284 4 ft3, how many bushels will the bin hold? Round to the nearest bushel.
   
   
    
   

Solution

1. When you look at the hopper, you can visualize that the portion holding the grain is made up of a large cone with a diameter of 14 ft minus a small cone with a diameter of 1.5 ft. In order to find the capacity of the hopper, you need to find the capacity of the large cone and then subtract the capacity of the small cone.
   
   To calculate these capacities, you still need to find the height of both cones. Use trigonometry to find the height of the large cone and the height of the small cone.
   
   
    
   
   
   
    
   
   
   

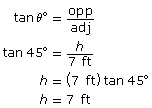
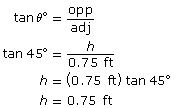
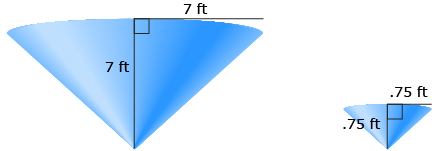
   Find the volume of the large cone with radius = 7 ft and height = 7 ft.
   
   
   

    
   
   
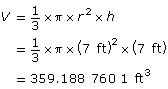
   Do not round until you have subtracted the smaller cone. Rounding may introduce unwanted errors at this stage.
   
   Find the volume of the small cone with radius = 0.75 ft and height = 0.75 ft.
   
   
    
   
   
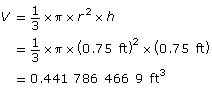
   The volume of the conical hopper is the difference between these volumes.
   
   
    
   
   
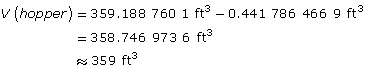
   The hopper can hold approximately 359 ft3 of grain.
   
   
2. 

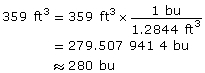
Self-Check 3

 

Work through Pyramid and Cones - Activity B. Complete the five assessment questions found at the bottom of the activity. You will check your answers in the activity.

Screenshot reprinted with permission of ExploreLearning.