Lesson 5

Discover

 

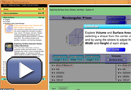
In Try This 1 you will discover the relationship between linear dimensions—length, width, and height—and corresponding changes in volume. You have previously used Exploring Surface Area, Volume, and Nets (Object Interactive). In Try This 1 you will use the applet again to see how volume is affected when you change one, two, or all three dimensions by a linear scale factor.

 

Try This 1

 

Use Exploring Surface Area, Volume, and Nets (Object Interactive) to answer the following questions. Note that in each case of Rectangular Prism, the starting point is a single cube. When the scale factor is 1, the dimensions (length, width, and height) are all 1.

1. Complete a table like the following. Some entries are filled in as examples.
   
   

   Scale Factor	Volume (in cm3) when the following dimension is multiplied by the linear scale factor   • only length	Volume (in cm3) when the following dimensions are multiplied by the linear scale factor   • length • width	Volume (in cm3) when the following dimensions are multiplied by the linear scale factor   • length • width • height
   1 (original cube)	1	1	1
   2	2	4	8
   3
   4
   k

If you need help answering the following questions, complete questions 1 and 2 in Are You Ready? This will help you see the pattern in the table.

2. How is the volume affected if only the length is changed by a factor of k?
   
   
3. How is the volume affected if both length and width are changed by a factor of k?
   
   
4. How is the volume affected if all three dimensions are changed by a factor of k?

Share 1

Share and discuss your responses to the questions in Try This 1 with a classmate or with a group of people. Summarize your discussions by answering the following question:

• What is the relationship between changes in linear dimensions and the effects of the changes on volume?

Save your responses to Try This 1 and a short summary of your discussion from Share 1 in your course folder.