Lesson 3

1. Lesson 3

1.7. Explore 3

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

When you are working with the unit circle, you know the equation for the circle is always x2 + y2 = 1. This is because the radius of the circle is 1. Could you determine if a point were on the unit circle if you knew both coordinates? Could you determine the x-coordinate if you knew the y-coordinate and that the point was on the unit circle?

Try This 3

Is the point 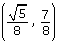on the unit circle?
You will determine the y-coordinate for all points on the unit circle if the x-coordinate of the point is .
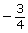1. Draw a diagram indicating where this point could be located on the unit circle.
2. Use the equation of the unit circle to help determine the y-coordinate.

Save your responses in your course folder.

Substitute the x-coordinate into the equation x2 + y2 = 1, and then solve for y. Remember that when you take the square root of a number, the answer could be positive or negative.

There is more than one point on the unit circle where the x-coordinate is . It's important that you get this answer correct. Check to see if your image matches the image shown here.

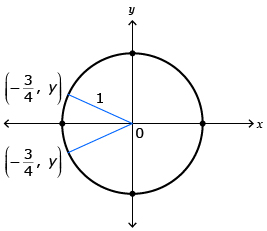
This is a picture of a circle on an x- and y-axis with the center at (0, 0) and radius of 1. There are two terminal arms, one in quadrant two and one in quadrant three. The two points that the terminal arms and circle intersect at are labelled negative 3 quarters and y.

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission.

Coordinates that are on the unit circle must satisfy the equation of the unit circle, x2 + y2 = 1.