Lesson 3
1. Lesson 3
1.2. Explore
Module 6: Measurement
Explore
tolerance: the range of acceptable dimensions
Source: MathWorks 12 Student Book/Teacher Guide.
(Vancouver: Pacific Educational Press, 2011.)
In the Discover activity, you may have noticed that some of the furniture pieces will fit through the door one way but not the other way. The doorway is only big enough for some of the pieces to be carried through. The range of measurements for the width and height of the door is called the tolerance.
Tolerance is highly important when it comes to industry and manufacturing.
To reduce the costs of manufacturing, blueprints are created to cover, in detail, all necessary materials and measurements. Since measurement tools have varying degrees of accuracy and precision, the measurements displayed on the blueprint must include some tolerance. The measurements are shown with a plus or minus (±) symbol to indicate the tolerance margin.
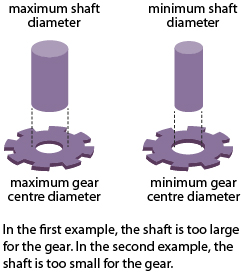
Extra consideration needs to be taken when determining measurement tolerances for manufacturing pieces that connect or slide against each other within the final product. For example, gears and shafts must align to fit one another.
The maximum diameter of the shaft must be able to fit into the minimum diameter of the gear’s centre, or vice versa, as shown in the illustration on the right.
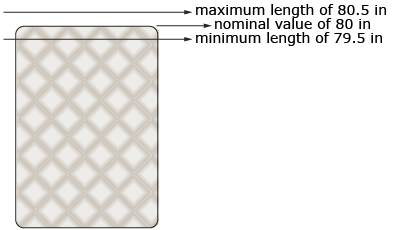
Blueprint measurements show a target for the measurement dimensions. The actual measurements must fall within the range of the target. For example, recall from Discover that the length of a king-size bed is 80 ± 0.5 in.
The nominal size is 80 in, and the tolerance is “plus or minus 0.5” in. This means that the actual manufactured bed should have a length that falls within 80 + 0.5 in and 80 − 0.5 in. The maximum value is 80.5 in, and the minimum value is 79.5 in.
Jupiterimages/ Photos.com/Thinkstock
There are always slight variations in the size of manufactured parts. Previously you were introduced to the term nominal value.
This term helps to describe manufacturing tolerance.
nominal value: the target value for the measured quantity
manufacturing tolerance: the difference between the maximum acceptable dimension and the minimum acceptable dimension
It can be expressed in several ways:
- nominal value
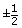(tolerance) - minimum value
- maximum value
Notice that the way a tolerance is written resembles the form in which measurement uncertainty is expressed. It is important to remember that a tolerance is not an uncertainty, but rather the acceptable range of a given measurement.
Source: MathWorks 12 Student Book/Teacher Guide.
(Vancouver: Pacific Educational Press, 2011.)
The following activity will allow you to explore the idea of tolerances and tolerance notation.
Try This 2
Open the interactive activity Tolerance Interval. This activity allows you to set a nominal value and tolerance for a centimetre ruler. The acceptable values then show up in red. When an object is clicked, a larger version will appear for you to measure. Use the interactive to answer the following questions.
- A hockey puck is supposed to have a diameter of 7.6 ± 0.2 cm. Is this size of hockey puck acceptable?
- A bakery wants its loaves of bread to be
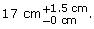Is the size of this loaf of bread acceptable? - Wrenches 1 and 2 are acceptable sizes, while wrenches 3 and 4 are not acceptable. Determine a possible tolerance for the wrench size.
- Determine a tolerance in the form
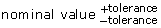so the difference between the minimum and maximum is 0.8 cm and the banana is the minimum acceptable value. - Determine a tolerance in the form
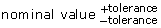so the difference between the minimum and maximum is 0.8 cm and the banana is the maximum acceptable value.
Save your responses in your course folder.
Share 2
With a partner or in a group, share your answers from Try This 2 and answer the following questions.
- Are there different ways that you could write solutions to questions 4 and 5 from Try This 2? Explain.
- Rewrite your solutions to questions 4 and 5 from Try This 2 using different nominal values.
Record your shared responses in your course folder.