Print this chapterPrint this chapter

Lesson 2

1. Lesson 2

1.6. Explore 2

Mathematics 30-2 Module 1

Module 1: Logic and Set Theory

 

To practise your knowledge of set terminology, complete the following interactive activity.

 

Self-Check 1

 

Marc Villick is a salesman at the car dealership in his town. He only sells new vehicles from his company manufacturer.

 

In the month of August, he sold 20 vehicles. The vehicles sold were two compact cars, four mid-sized cars, three vans, eight SUVs, and three 4 × 4 crew-cab trucks.

 

Here are the colour selections the customers chose.

 

Vehicle Type Colour
2 compact cars

1 red and 1 white
4 mid-sized cars

1 yellow, 2 white, and 1 tan
3 vans

1 white and 2 red
8 SUVs

4 tan, 2 white, and 2 blue
3, 4 × 4 crew-cab trucks

2 white and 1 black


Go to Venn Vehicles and complete the drag-and-drop activity.

 

 

This is a play button for Venn Vehicles.

You may have noticed in your textbook and from previous courses that sets are often given a single letter name and described by listing the elements between the symbols { and }. This is the formal notation (i.e., symbols) that mathematicians use when describing sets. The following are examples of sets using this notation.

 

This is a photo of a map of Canada.

Adapted from base map © Map Resources

 

Word Description Set Notation

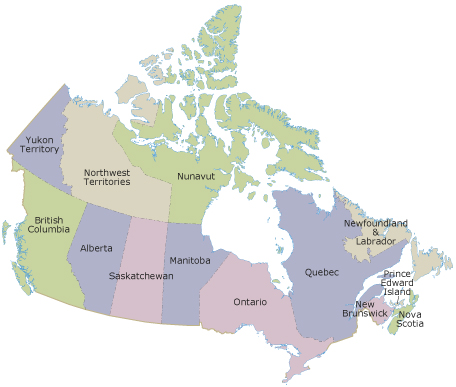
universities Analiese is considering for medicine programs

M = {Alberta, Saskatchewan, British Columbia, Calgary, Montreal}

even numbers

E = {2, 4, 6, 8, …}

multiples of 6 less than 20

S = {6, 12, 18}

provinces west of Ontario

P = {British Columbia, Alberta, Saskatchewan, Manitoba}

western provinces with mountain ranges

W = {British Columbia, Alberta}

There are two more symbols used by mathematicians when describing sets.

  • subset: ⊂

    For example, W (western provinces with mountain ranges) is a subset of P (provinces west of Ontario). The symbolic way to write this is W ⊂ P.
  • complement: A′

    The letter A is the name of the set, and the prime symbol ′ indicates complement.

Try This 2

 

The following sets of numbers are described using standard set notation. Using words, describe what numbers are contained in each set. List the elements. Note: You can scroll your mouse over different highlighted areas of the set descriptions for questions 2 and 3 to read hints.

  1. A = {1, 2, 3, …, 20}
  2. B = {x   |   1 ≤ x ≤ 20,  x ∈ N}
  3. C = {c   |   c = 2x, 0 ≤ x ≤ 20, x ∈ W}

course folder Save your responses in your course folder.

 

Share 2

 

What words or symbols used in Try This 1 are similar to those discussed in Try This 2?

 

course folder If required, save a record of your discussion in your course folder.
The variable x can only take on values from the set of whole numbers.
The variable x takes on all values where 0 is less than or equal to x and x is less than or equal to 20.

This is shorthand for saying x takes on all values from 0 to 20, inclusive.
c is equal to 2 times x
such that
Each element of the set can be described by the variable c.
The variable x can only take on values from the set of natural numbers.
The variable x takes on all values where 1 is less than or equal to x and x is less than or equal to 20.

This is shorthand for saying x takes on all values from 1 to 20 inclusive.
such that
Each element of the set can be described by the variable x.
Each element of the set can be described by the variable x.