Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.2. Explore

Mathematics 30-2 Module 1

Module 1: Logic and Set Theory

 

Explore

 

The sports example from the Focus section is an example that involves the intersection of sets and the union of sets. Examples in previous lessons also included intersections and unions; however, in this lesson you will examine intersections and unions in more detail.

 

The set of elements that are common to two or more sets is called the intersection of those sets. Mathematicians use the symbols A ∩ B to signify the intersection of sets A and B.1 Sets that have no elements in their intersection are said to be disjoint.

 

All elements that are counted are considered to be in the universal set. This is usually represented by drawing a box around the Venn diagrams. The universal set can be thought of as the set that contains all other sets. For example, if the set C = {consonants}, the universal set is the alphabet.

 

You may also find a set that has no elements in it. This is known as the empty set or null set. For example, for the set X = {days of the week starting with the letter “J”} is an empty set. An empty set is written as { }, so, for the example, this would be written as X = { }.

 

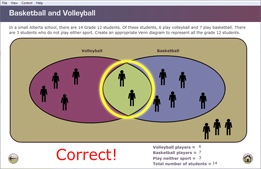
This is a Venn diagram showing two overlapping sets: volleyball and basketball. There are four stickmen in the volleyball-only region, five in the basketball-only region, two in the intersection (which is shaded yellow), and three in neither volleyball nor basketball.

In the sports example from Focus, there are two students in the intersection of the volleyball and basketball sets, as shown by this Venn diagram.

 

The set of all elements in two or more sets is called the union of those sets. Mathematicians use the symbols A ∪ B to signify the union of sets A and B.2

 

tip bar
One way to remember that ∪ signifies union is that the symbol looks like a capital letter U, which is the first letter of union.

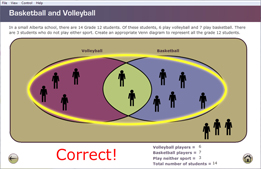
In the sports example from Focus, there are eleven students in the union of the volleyball and basketball sets, as shown by the following Venn diagram.

 

This is a Venn diagram showing two overlapping sets: volleyball and basketball. There are four stickmen in the volleyball-only region, five in the basketball-only region, two in the intersection, and three in neither volleyball nor basketball. The volleyball and basketball ovals are both shaded yellow.

 

The following examples may help you understand these terms better.

 

Sets Intersection Union

F = {red, blue, green}

H = {red, purple}

F ∩ H = {red}

F ∪ H = {red, blue, green, purple}

A = {1, 2, 3, 4}

B = {3, 4, 5}

A ∩ B = {3, 4}

A ∪ B = {1, 2, 3, 4, 5}

J = {1, 3, 5, 7}

B = {2, 4, 6, 8}

J ∩ B = { }

There are no elements in this set. (It is the empty set.) Therefore, sets J and B are disjoint.

J ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}


textbook

You may also want to read “Communication: Notation” on page 23 of your textbook for descriptions of union and intersection using Venn diagrams. Note how the textbook explains that the notation A \ B is read as “A minus B” to signify the set of elements that are in set A but not in set B.

Self-Check 1
  1. Complete “Check Your Understanding” questions 1 and 2 on page 32 of your textbook. Note: For question 2, you may want to complete part b. first and then use the Venn diagram to answer part a. Answers
  2. Complete “Practising” question 6 on page 33 of your textbook. Answers

1, 2Adapted from PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.