Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.3. Explore 2

Mathematics 30-2 Module 1

Module 1: Logic and Set Theory


Now some terminology is required to describe the sports problem from Focus. You may have discovered that the total number of students playing volleyball or basketball is not simply the sum of students playing volleyball and students playing basketball. This can be written using set notation as

 

 

n(volleyball ∪ basketball) ≠ n(volleyball) + n(basketball)

 

The reason for this is that students who play both volleyball and basketball will be counted twice—once when counting the volleyball players and once when counting the basketball players. To get a correct total, you must subtract the number of students that play both sports—the intersection of those two sets. Using set notation, this becomes the following:

 

 

n(volleyball ∪ basketball) = n(volleyball) + n(basketball) − n(volleyball ∩ basketball)

 

Mathematicians call this the principle of inclusion and exclusion. For any sets A and B, the following is always true:

 

 

n(A ∪ B) = n(A) + n(B) − n(A ∩ B)

 

To learn more, view the multimedia piece titled Principle of Inclusion and Exclusion.

 

 

This is a play button for Principle of Inclusion and Exclusion.



textbook

For further information about the principle of inclusion and exclusion, you may wish to read “Need to Know” on page 31 of your textbook.

Self-Check 2
  1. A group of 28 adults were surveyed about their game-playing habits. The results are shown in the Venn diagram.

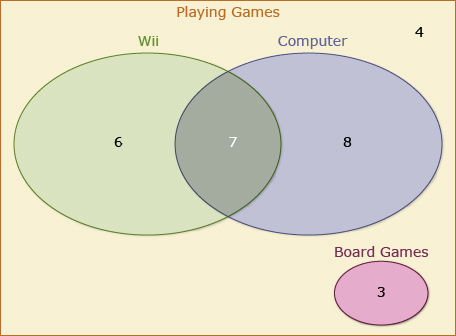
    This is an image of a Venn diagram showing different game-playing habits.

    Using the following set notation, answer the questions.

    P = {all adults surveyed}
    W = {adults who play the Wii}
    C = {adults who play on the computer}
    B = {adults who play board games}
    1. n{W ∪ C}
    2. n{W \ C}
    3. n{W ∩ C}
    4. n{W ∩ B} (What are sets W and B called in relation to each other?)
    5. Describe the elements in the complement of {W ∪ C}.

    Answers

 

textbook

  1. Complete “Practising” questions 8 and 9 on page 33 of your textbook. Answers

So far, this lesson has described unions and intersections as they relate to set theory application. In the next Try This activity, you will see the use of new terms that are connected to union and intersection. The new terms are and, or, and not.

 
Try This 2

 

When studying the relationship between the union and intersection of sets, there is some new terminology you need to be comfortable using correctly.

 

The short multimedia piece titled And, Or, and Not will introduce you to the use of the words and, or, and not in the context of union and intersection of sets seen earlier in the Basketball and Volleyball example.

 

 

This is a play button for And, Or, and Not.