Lesson 1

When you encounter a rational expression where both the numerator and denominator must be factored before the expression can be simplified, it is possible that they will share a common factor. You can use this knowledge to factor more easily.

Suppose you are required to simplify the following rational expression:

Step 1: Start by factoring the numerator.

Step 2: Since the numerator has a binomial factor of (a − 1), there is a chance that the denominator will also have the same factor. If so, you will have the following:

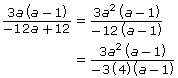
Why did the signs of the terms in the denominator change?

Step 3: You should check that −12 is the second factor by multiplying −12 and (a − 1). In this case, the product is −12a + 12. Therefore, the correct factors are −12 and (a − 1). Now you can use the property of 1 to simplify the expression.