Lesson 2

You can use a graphing calculator to check if two expressions are equal. For example, you may wonder if the solution 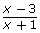is equal to 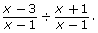Graph both of these on the same screen by inputting the following:

 

 

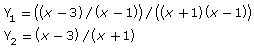
Be very careful when inputting the expressions into your calculator. Make sure you put brackets where appropriate to ensure that the calculator performs the correct order of operations. If the two expressions are equal, the graphs will be the same. For some calculators, you can change the thickness of a graph so that you can see more clearly that the two graphs are, in fact, identical.

In Try This 5 you uncovered a pattern for dividing rational expressions; but when you divide rational expressions, the non-permissible values must be identified. In Try This 6 you will explore how non-permissible values are found when dividing rational expressions.

Try This 6

1. Complete a table of values like the one shown for the two rational expressions. In the first row, state the non-permissible values determined by looking at the denominators. In the next rows, substitute in the given values of x and calculate the value of the rational expression.

    

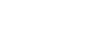
   non-permissible values determined by looking at the denominators
   x = −2
   x = −1
   x = 0
   x = 1
   x = 2
   x = 3

2. What do you notice about the values in the table?
3. From the table, what are the non-permissible values of the two expressions?
4. When dividing rational expressions, where are the non-permissible values located? Is it sufficient to look at the denominators only?

Save your work in your course folder.