Lesson 3
1. Lesson 3
1.11. Explore 7
Module 5: Rational Expressions
You saw in Try This 5 that when adding rational expressions with different denominators, you need to first find a common denominator. Adding Fractions illustrates this process.
Consider the following example:
![]()
The first step is always to state the non-permissible value. Looking at the denominators, you can see that a ≠ 0.
Next, find the lowest common denominator. Find the prime factorization of each denominator.
15a = 3 × 5 × a
5a2 = 5 × a × a
Therefore, the LCD is 3 × 5 × a × a = 15a2.
Multiply each expression by a fraction that is equal to 1, so each expression has the denominator 15a2.
![]()
Now each denominator is the same. Simplify.
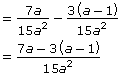
Subtract the numerators.
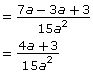
Make sure to include the restrictions from the original expressions.
![]()
Self-Check 2
Complete questions 1.a., 1.b., and 4 on page 249 of the textbook. Answers
