Lesson 4

1. Lesson 4

1.8. Explore 4

Mathematics 30-2 Module 5

Module 5: Rational Expressions

You have now learned the basics of solving rational equations. You can apply the principles you have learned to other rational equations. In order to identify the lowest common denominator more easily, try factoring the denominators. Keep this in mind as you complete Try This 4.

Try This 4

Study the following rational equation:

How would you solve this equation? The approach you learned previously can be applied here. Create a table like the following, and complete the steps to determine the solution.

Step	Your Work
Step 1: Determine the non-permissible values.
Step 2: Determine the LCD.
Step 3: Multiply by the LCD.
Step 4: Solve for x.
Step 5: Check your solutions to see if they are extraneous.

Save your work in your course folder.

Share 2

With a partner, discuss the following questions.

Compare and contrast the work required to solve 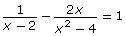to the work that was required to solve 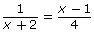in Try This 2.
In the last step, you should have obtained two possible roots. However, did you notice that one of the roots is also a non-permissible value? What does this imply?

If required, save your responses in your course folder.

Remember that an extraneous solution is a non-permissible solution to the original rational equation.

What method of solving a quadratic equation is appropriate here?

What is the resulting equation when the LCD is applied to each term of the expression, including the term on the right side of the equation?

What binomial factors are required in the LCD?

How does factoring help you to identify the non-permissible values?