Print this chapterPrint this chapter

Lesson 2

1. Lesson 2

1.5. Explore

Mathematics 30-2 Module 7

Module 7: Exponents and Logarithms

 

Explore

 

This is a picture of some rod-shaped bacteria.

Hemera/Thinkstock

In Try This 1 you were working with an exponential equation. An exponential equation has a variable in the exponent. An example would be 5x = 25x − 1 because the variable x is an exponent.

 

In Try This 1 you attempted to solve the number of 20-minute intervals needed to produce a certain number of bacteria. You may have used an algebraic method or a graphical method to solve the problem. In Try This 2 you will try to solve exponential equations using an algebraic method.

 

One algebraic method you may have used in Try This 1 was writing each side of the equation as powers with the same base. To solve question 2, for example, 256 = 2t, you may have used a method similar to the following:

 

 

 

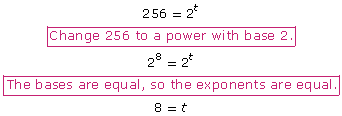
Notice from the example that if the bases of two equal powers are the same, then the exponents must be equal. Keep this important idea in mind as you complete Try This 2.

 

Try This 2

  1. Solve for x in the equation 4x = 64. Describe how you solved for the value of x.
  2. Solve for x in the equation 4x − 2 = 64. Describe how you solved for the value of x.
  3. Solve for x in the equation 4x + 5 = 642x. Describe how you solved for the value of x. Verify your solution.

course folder Save your responses in your course folder.

When the bases are the same on the left and right sides of the equation, make the exponents equal to each other and solve for x.
Try to write 64 as a power with base 4 and then solve for x.
When you write 64 as a power with base 4, you will have a power to a power. The exponent laws state to multiply the exponents in this situation.