Lesson 2
1. Lesson 2
1.7. Explore 3
Module 7: Exponents and Logarithms
In Try This 2 you looked at solving exponential equations algebraically by writing each side of the equation with equivalent exponents that had the same base. In Try This 3 you will explore how to solve exponential equations graphically.
Try This 3
iStockphoto/Thinkstock
The medical isotope iodine-131 is produced at Chalk River Laboratories in Ontario and is used in imaging and diagnosing thyroid problems. A radioactive sample of iodine-131 has a half-life of 8 days. This means that after 8 days, half of the original amount of the sample has decayed.
The equation that can be used to describe the half-life function is
![]()
where A is the remaining mass of iodine-131, A0 is the original mass of iodine-131, and t is the time in days.
- Notice that in the function
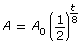 , the value of parameter b is
, the value of parameter b is 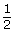 . Can you determine if this is exponential growth or exponential decay? Explain your reasoning.
. Can you determine if this is exponential growth or exponential decay? Explain your reasoning. 
- How long would it take a 4.0-g sample of iodine-131 to decay to 0.25 g?
- Determine the time algebraically.

- Determine the time using a graph. Describe the process you used.

- Determine the time algebraically.
![]() Save your responses in your course folder.
Save your responses in your course folder.