Lesson 5

1. Lesson 5

1.2. Explore

Mathematics 30-2 Module 7

Module 7: Exponents and Logarithms

Explore

This photo shows a policeman giving a halt gesture. It reads “Obey the law… of logarithms.”

Adapted from Brand X Pictures/Thinkstock

In Discover, you may have found that logarithms can be added or subtracted using laws similar to

log M + log N = log(M × N)

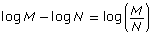
These rules can be extended to any base to give

logb M + logb N = logb(M × N)

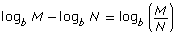
Notice that the bases must be the same to use these laws. The same restrictions apply to these rules as to other logarithms: b, M, and N are real numbers greater than 0, and b ≠ 1.

The following table provides an explanation of how the logarithmic laws are related to exponential laws. Remembering that a logarithm is an exponent may help you interpret the table.

Law of Logarithms	Law Expressed Mathematically	Pattern Explained by the Law of Powers
product law of logarithms	logb (M × N) = logb M + logb N	In the product law of powers, (bm)(bn) = bm + n, the exponents are added. In the product law of logarithms, logb (M × N) = logb M + logb N, when you are multiplying two terms in a single logarithm, it is the same as adding the logarithms of each term.
quotient law of logarithms		In the quotient law of powers, , the exponents are subtracted. In the quotient law of logarithms, , when you are dividing two terms in a single logarithm, it is the same as subtracting the logarithms of each term.