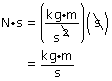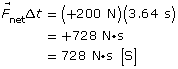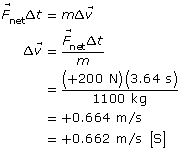Module 1
1. Module 1
1.8. Page 3
Module 1—Momentum and Impulse
Impulse
© Courtesy of ADAC.de
impulse: the product of the net force applied to an object and the time interval during an interaction
The equation is as follows:
Whether you stop a crash test dummy in a vehicle with an airbag or stop a putty ball with a cushioned surface, the combination of force acting over a time interval plays the essential role. That is why the product of the force and the time interval during which the force acts is given a special name—impulse.
|
|---|
The unit for impulse is N·s, which is the same as the unit for momentum, kg·m/s, since N = kg·m/s2.
|
DID YOU KNOW?
Impulse is a different kind of quantity because it does not have its own symbol. Instead, impulse is either represented by the word impulse or the variables 
This helps remind you that many combinations of a force acting over a time interval can provide a specific amount of impulse.
Read
You can learn more about impulse and how it can be calculated by reading pages 457, 458, and the top half of page 459 in your textbook. Pay particular attention to the calculations shown in “Example 9.3.”
SC 3. Use Newton's second law to identify the two different ways of calculating impulse.
SC 4. Complete the following chart to summarize the symbols and units for each of the quantities that you have learned so far in this module.
Quantity |
Symbol |
SI Unit |
|---|---|---|
impulse |
||
net force |
||
time interval |
||
momentum |
||
mass |
||
velocity |
SC 5. Do “Practice Problems” 1 and 2 on page 458 of your textbook.
Self-Check Answers
SC 3.
The following equations show how Newton's second law reveals two ways of calculating impulse.
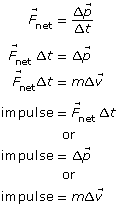
SC 4.
Quantity |
Symbol |
SI Unit |
|---|---|---|
| impulse |
|
N·s or kg·m/s |
| net force |
|
N |
| time interval |
|
s |
| momentum |
|
kg·m/s |
| mass | m |
kg |
| velocity |
|
m/s |
Note that impulse, net force, momentum, and velocity are all vector quantities, so the symbol for each of these quantities includes an arrow.
SC 5.
Solution to Problem 1
Given
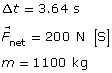
Required
-
the impulse provided to the car,
-
the change in velocity of the car,
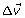
Analysis and Solution
Let south be the positive direction.
Paraphrase
The impulse provided to the car is 728 N·s [S].
The velocity of the car changes by 0.662 m/s [S].
Solution to Problem 2
Given
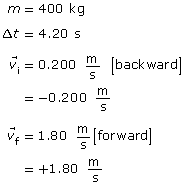
Required
The average net force acting on the dog team.
Analysis and Solution
Let forward be the positive direction.
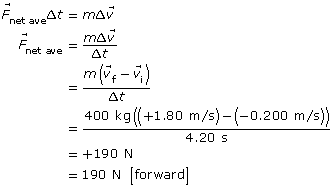
Paraphrase
The net force acting on the dog team is 190 N [forward].
Module 1: Lesson 2 Assignment
Remember to submit the answers to A 1 and A 2 to your teacher as part of Module 1: Lesson 2 Assignment.
A 1. An arrow gains a momentum of 94.3 kg·m/s [W] in 0.400 s. Determine the magnitude and direction of the average unbalanced force acting on the arrow.
A 2. An artillery shell is accelerated from rest and gains a momentum of 2.00 x 103 kg·m/s [E]. If the average net force acting on the shell is 8.50 x 103 N [E], then calculate the time interval that this net force acts on the shell.
Calculating Impulse from Graphs
© Bodil1955/shutterstock
When the archer in this photograph releases the arrow, the force exerted by the bow on the arrow will not be constant. The following graph shows the magnitude of the net force on the arrow during the first part of its release. How do you think you could determine the magnitude of the impulse in a case like this?
Read
You can find out more about how to determine the magnitude of the impulse from a force-time graph by reading from the middle of page 459 to the bottom of page 460.
Self-Check
SC 6. Return to the graph describing the net force on the arrow vs. time shown earlier in this lesson. Use the information on that graph to determine the magnitude of the impulse acting on the arrow.
Self-Check Answer
SC 6.
Given
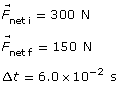
Required
The magnitude of the impulse, 
.
Analysis and Solution
The magnitude of the impulse is equal to the area under a net force versus time graph.
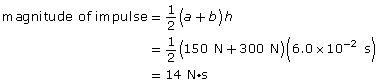
Paraphrase
The magnitude of the impulse is 14 N·s.
Read
You can use the area under a graph to determine the magnitude of impulse. However, in some circumstances, the area under the graph is not easy to determine. Read pages 461 and 462 of your textbook to learn more about applications and limitations. Pay close attention to “Example Problem 9.4.”
Try This
TR 1. Solve practice problem 1 on page 462 of your textbook.
TR 2. How can you get a negative area on a graph and what does it mean in terms of impulse?
Module 1: Lesson 2 Assignment
Remember to submit the answers to A 3 to your teacher as part of Module 1: Lesson 2 Assignment.
A 3. A high school football player hits and pushes a tackling dummy during practice. The following graph shows the amount of net force that acts on the player.
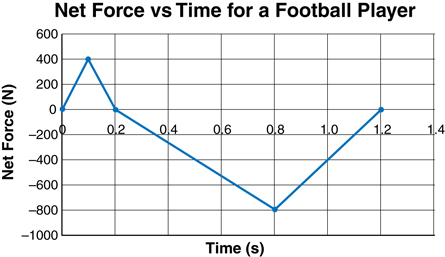
- What happens to the player’s forward velocity during the first 0.20 s?
- What happens to the player’s velocity from 0.20 to 1.20 s?
- What is the impulse that acts on the football player?
- If the 60-kg player is running forward at 7.0 m/s when she makes contact with the dummy, what is the player’s velocity at the end of the 1.20 s impact?