Module 2

Module 2—The Conservation of Momentum in Isolated Systems

Describing Momentum Using Vector Components

 

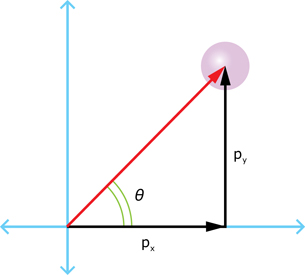
Any two-dimensional vector, such as momentum, can be resolved into components. Generally, we resolve vectors into horizontal (x) and vertical (y) components. The diagram to the right shows a vector, , resolved into its x and y components. Using this diagram and some basic trigonometric identities (sin, cos, tan), answer the Self-Check questions below.

 

Self-Check

 

SC 1. What is the expression that gives px as a function of  and θ?

 

SC 2. What is the expression that gives py as a function of and θ?

 

SC 3. Write a general expression for , if both px and py are known.

 

SC 4. If both px and py are known, what is the general expression for θ?

 

 

 

Analyzing Collisions Using Component Analysis

 

See this demonstration of adding vectors for a 2-D collision. Applying the law of conservation of momentum in two-dimensional collisions is more complex than that of a one-dimensional collision. Essentially, the law of conservation of momentum is applied twice—once in the x and once in the y directions. Following is an example of how to apply the law of conservation of momentum correctly to solve two-dimensional collision problems.

 

Example Problem

 

An 8.0-kg mass collides elastically with a 5.0-kg mass that is at rest. Initially, the 8.0-kg mass was travelling to the right at 4.5 m/s. After the collision, it is moving with a speed of 3.65 m/s and at an angle of 27° to its original direction.

 

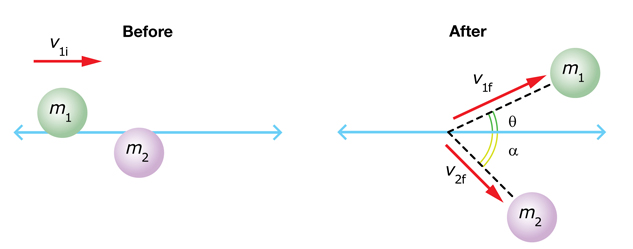
What is the final velocity for the 5.0-kg mass?

 

Example Solution

 

Given

 

mass 1 m1 = 8.0 kg 

 

initial velocity of mass 1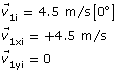 

 

final velocity of mass 1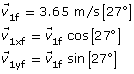

 

mass 2 m2 = 5.0 kg

 

initial velocity of mass 2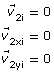

 

Required

 

The final velocity of mass 2, .

 

Analysis and Solution

 

Initially, mass 1 moves to the right, and mass 2 is at rest. Thus, the total momentum is in the x direction (to the right). After the collision, mass 1 travels at an angle of 27° to its original direction of motion; it now has momentum in the y direction as well as the x direction. For momentum to be conserved, mass 2 must have momentum in both the x and y directions.

 

Define motion to the right as positive, which follows the usual convention. As well, measure angles counterclockwise from the horizontal.

 

Use the law of conservation of momentum to solve this question. Since momentum is conserved in both the x and y directions, we can set up two sets of equations—one each to solve for v2fx and v2fy.

 

Conservation of momentum in the x direction:

 

 

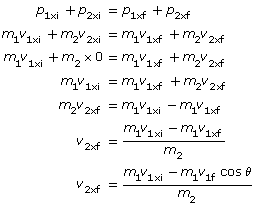
Conservation of momentum in the y direction:

 

 

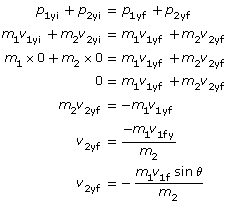
The final velocity for mass 2 in the x direction:

 

 

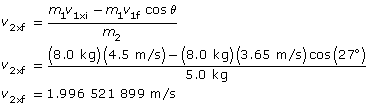
The final velocity for mass 2 in the y direction:

 

 

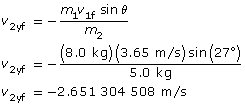
Once you know the final velocity in the x and y directions, you can find the final velocity and direction of motion for mass 2. Remember, do not use the rounded off values in your calculations—use rounded numbers for the final paraphrase.

 

Final velocity for mass 2:

 

 

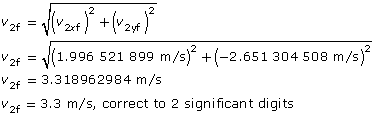
Direction of motion:

 

 

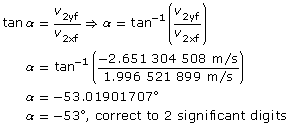
This answer seems to make sense—mass 2 has to move to the right and down in order to conserve momentum. Furthermore, this answer can be verified with the simulation. Check it yourself!

 

Paraphrase

 

The final velocity of mass 2 is 3.3 m/s [−53°] or 3.3 m/s [307°].

 

Try This

 

TR 2.A 9.0-kg ball is travelling to the right at 8.0 m/s until it impacts a 3.0-kg stationary ball. After the collision, the 9.0-kg ball is travelling at 5.61 m/s at an angle of 7.8º above the horizontal. Calculate the velocity of the 3.0-kg ball after the impact. (Note: To view and verify this collision using the simulation, open the “Options” () and set e = 0.44. Then set the blue mass to 9.0 kg and the green mass to 3.0 kg.)

 

Read

 

Read “Collisions in Two Dimensions” on pages 487 to example 9.14 on page 495 of your physics textbook.

 

Module 2: Lesson 3 Assignment

 

Remember to submit the answers to A 1 and A 2 to your teacher as part of your Module 2: Lesson 3 Assignment.

 

A1. A car with a mass of 1400 kg is westbound at 50 km/h. It collides at an intersection with a northbound truck having a mass of 2000 kg and travelling at 40 km/h. What is the initial common velocity of the car and truck immediately after the collision if they have an inelastic collision?

 

A2. A police car with a mass of 1460 kg is headed west at 60 km/h when it has an inelastic collision with a southbound 2000-kg ambulance. The wreckage ended up travelling at 45 km/h at 236°. What was the initial speed of the ambulance?

 

Read

 

Read “Elastic and Inelastic Collision in Two Dimensions” on pages 495 to 498 of your physics textbook.

 

Try This

 

TR 3. Answer questions 1 to 4 in “9.4 Check and Reflect” on page 499 of your physics textbook.

 

Module 2: Lesson 3 Assignment

 

Remember to submit the answers to A 3 and A 4 to your teacher as part of your Module 2: Lesson 3 Assignment.

 

A3. A billiard cue ball with a mass of 0.60 kg and an eight ball with a mass of 0.55 kg are rolled toward each other. The cue ball has a velocity of 3.0 m/s at 360°, and the eight ball has a velocity of 2.0 m/s at 90°. After the collision, the cue ball moves off at a velocity of 2.0 m/s at 40°.

1. What is the velocity of the eight ball?
2. Prove whether or not the collision is elastic.

A4. A proton with an initial velocity of 2800 m/s [90°] is struck by a neutron heading at 320° with a speed of 2900 m/s. The neutron bounces off of the proton with a velocity of 1864 m/s [270°].

1. What is the final velocity of the proton?
2. Prove whether or not the collision is elastic.

Physics 30 Learn EveryWare © 2009 Alberta Education