Module 3

1. Module 3

1.11. Page 2

Module 3 Lesson 2

Module 3—Electrical Phenomena

Explore

A photo shows a segment of Earth and its atmosphere seen from space, with a quarter moon above.

A Link Between Electrostatics and Gravitation

Coulomb did not begin his work on determining the electric force law on his own. As the following timeline indicates, other scientists had already done much of the essential groundwork. You might be surprised to know that the essential ideas came from Isaac Newton’s work on gravitation.

Date	Scientist	Contribution to Coulomb’s Work
1687	Isaac Newton	Published his great book Mathematical Principles of Natural Philosophy, which included his three laws of motion and his law of universal gravitation:
1775	Benjamin Franklin	Franklin noticed that a small cork inside a hollow, charged can experiences no force. The same cork experiences a force outside the can. He wrote to Joseph Priestly and asked him to repeat the experiment.
1776-1777	Joseph Priestley	Priestley verified Franklin’s results and realized a connection to Newton’s law of universal gravitation. Newton had explained in his book that an object would experience no force of gravity inside a hollow planet. He was able to show that this was the consequence of the “inverse squares law,” which says that gravitational force acting on two masses is inversely proportional to the square of the distance between their centres. Priestly instantly likened the cork to the object and the hollow can to the planet. Priestley suggested that this indicated that the force of electricity could also be an inverse square law.

Date

Scientist

Contribution to Coulomb’s Work

1687

Isaac Newton

Published his great book Mathematical Principles of Natural Philosophy, which included his three laws of motion and his law of universal gravitation:

1775

Benjamin Franklin

Franklin noticed that a small cork inside a hollow, charged can experiences no force. The same cork experiences a force outside the can. He wrote to Joseph Priestly and asked him to repeat the experiment.

1776-1777

Joseph Priestley

Priestley verified Franklin’s results and realized a connection to Newton’s law of universal gravitation. Newton had explained in his book that an object would experience no force of gravity inside a hollow planet. He was able to show that this was the consequence of the “inverse squares law,” which says that gravitational force acting on two masses is inversely proportional to the square of the distance between their centres.

Priestly instantly likened the cork to the object and the hollow can to the planet. Priestley suggested that this indicated that the force of electricity could also be an inverse square law.

Read

To review the key features of Newton’s law of universal gravitation and to better understand what it means to say that this law is an “inverse square law,” read “10.2 Coulomb’s Law” on page 524 of your textbook. Pay special attention to the “Physics Insight” on the left-hand side of the page.

Self-Check

You can check your understanding by answering these questions:

SC 1. List all the variables that influence the magnitude of the force of gravity.

SC 2. Describe how increasing the size of both masses influences the magnitude of the force of gravity.

SC 3. Describe how increasing the distance (r) between the two masses influences the magnitude of the force of gravity

SC 4. Mathematically express how increasing the size of both masses influences the magnitude of the force of gravity. In other words, write a proportionality statement.

SC 5. Mathematically express how increasing the distance (r) between the two masses influences the magnitude of the force of gravity. In other words, write a proportionality statement.

Check your work.

Self-Check Answers

SC 1. The magnitude of the force of gravity is affected by the mass of the two objects and the distance between their centres.

SC 2. As the masses increase, the force increases. This is a direct relationship.

SC 3. As the distance (r) between the two masses increases, the magnitude of the force of gravity decreases. This is an inverse square relationship.

SC 4.

SC 5.

Making Predictions about the Electrostatic Force

Two large metal spheres are shown with electric discharge streamers arcing from one sphere to the other.

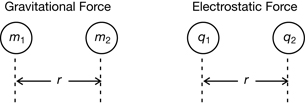
Given your answers to the previous questions, you should be able to speculate about the nature of the electrostatic force. The following graphic shows the possible connections between the gravitational force acting on two masses (m1 and m2) and the electrostatic force acting on two charges (q₁ and q₂).

The illustration is a comparison between the force of gravity and the electrostatic force.

Try This

TR 1. Identify the variables that will likely influence the magnitude of the electrostatic force.

TR 2. Speculate on how increasing the size of charges q1 and q2 will influence the size of the electrostatic force.

TR 3. Speculate on how increasing the distance between the two charges would influence the magnitude of the electrostatic force.