Module 3

1. Module 3

1.18. Page 2

Module 3 Lesson 3

Module 3—Electrical Phenomena

Explore

An Equation for Coulomb’s Law

A single bolt of lightning is shown striking a settlement on the distant shore of a large lake.

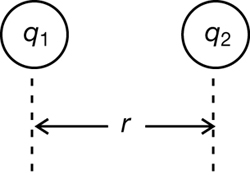
How would you describe the amount of charge delivered in a lightning strike or calculate the forces that act on the tiny charged particles within a crystal? You need values that can be described with units of measure and an equation for the electrostatic force. In the last lesson you learned that Coulomb’s work enabled him to describe the factors that affected the magnitude of the electrostatic force.

Although this mathematical expression describes Coulomb’s law, it is not an equation. The left-hand side does not equal the right because a proportionality constant (k) is missing. The proportionality constant enables the left side to be equal to the right by taking into account the units for charge, distance, and force.

Read

You can learn how units were considered in building the equation for Coulomb’s law by reading from the top of page 529 to the middle of page 530 in your textbook.

Self-Check

You can check your understanding by answering these questions.

SC 1. Complete the following graphic to summarize the quantities in the equation for Coulomb’s law as well as the units for each of these quantities.

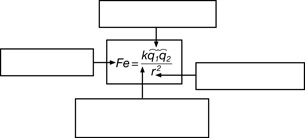
The illustration summarizes Coulomb’s law.

Quantity	Units
electrostatic force	Newtons (N)
Coulomb’s constant
charge
distance

SC 2. Provide two examples that illustrate the size of a coulomb as a unit for charge.

Check your work.

Self-Check Answers

SC 1.

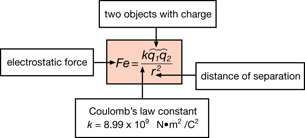
The illustration summarizes Coulomb’s law and shows the answers in the blank boxes.

Quantity	Units
electrostatic force	Newtons (N)
Coulomb’s constant
charge	coulombs (C)
distance	metres (m)

SC 2. The coulomb is a huge unit of charge. It is the amount of charge that could be transferred in a lightning strike. Alternatively, a coulomb corresponds to the amount of charge on 6.25 × 1018 electrons.

The photo shows the entirety of a long, branched piece of glass that shows the path of the lightning through the ground.

Photo by Stan Celestian, Glendale Community College Arizona.

Try This

TR 1. Starting with Coloumb’s law derive the units for Coulomb’s constant .

As you saw in Get Focused, this piece of glass was formed as lightning penetrated sand. The presence of air and moisture in the silica resulted in an explosive expansion of the silica as many coulombs of charge surged into the ground. Note the swollen lumps formed by the rapid expansion of super hot bubbles. This sample is, in fact, hollow—a fragile glass tube.

The precise arrangement of the silicon and oxygen atoms within the glass crystals is a consequence of Coulomb’s law. However, the analysis is quite complex, requiring you to consider the vector nature of forces.

To prepare for this, the next part of this lesson will lead you through a series of examples that will gradually increase in complexity. By the time you have completed the last example, you should be ready to revisit the arrangement of the atoms in the crystal of glass.