Module 3
1. Module 3
1.20. Page 4
Module 3—Electrical Phenomena
Calculations with Coulomb’s Law
Three Charges Forming a Line
If there are three charges arranged along a straight line, then the calculation of the net electrostatic force on any one of the three charges requires you to take into consideration the vector nature of forces.
Read
Read the first two paragraphs on page 532 of your physics textbook, and then read “Example 10.3.” Be sure to follow the solution carefully.
Self-Check
Use these questions to confirm your understanding of “Example 10.3.”
SC 5. Complete “Practice Problems” 1 and 2 on page 532 of your textbook.
Self-Check Answers
SC 5.
- The fact that sphere A and sphere C have the same charge means that the distance of separation is the only factor that will produce a difference in the electrostatic forces. In this case, the fact that the force varies inversely with the distance squared provides the key to drawing the free-body diagram. Since sphere C is two times farther away than sphere A, the electrostatic force exerted by sphere C must be (
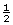)2 or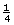 
as large as the electrostatic force exerted by sphere A.
This explains why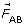
is four times longer than 
.
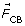- The net electrostatic force on sphere B is represented by a vector three units long directed to the left. This is the result of the vector addition of 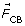, which is one unit long and directed to the right, combined with 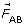which is four units long and directed to the left.
In the previous example and the practice problems, the fact that two of the charges had the same magnitude allowed symmetry to simplify the solution. The next problems are slightly more complex because this symmetry is not present.
Read
Do “Example 10.4” on page 533 of your textbook. Be sure to follow the solution carefully.
Self-Check
Use this question to confirm your understanding of “Example 10.4.”
SC 6. Complete “Practice Problem” 1 on page 533 of your textbook.
Module 3: Lesson 3 Assignment
Remember to submit your answers to A 2 and A 3 as part of your Module 3: Lesson 3 Assignment to your teacher for marks.
A 2. Do “Applications” problem 8 on page 538 of your textbook.
A 3. Do “Knowledge” problem 13 on page 540 of your textbook.
Did You Know?
Some samples of the glass formed by lightning strikes can be thousands or even millions of years old. When the glass was formed, miniscule bubbles of trapped gases were sealed within the delicate glass linings. In a sense, these structures can be thought of as a collection of miniature sealed test tubes, storing pockets of gas that reflect the condition of soil and atmosphere very long ago. Scientists studying long-term patterns of climate change are beginning to utilize “lightning glass” as a potential source of data.
Photos provided by Stan Celestian, Glendale Community College Arizona.
Calculations with Coulomb’s Law
Three Charges Forming a Triangle
The glass crystal from the Get Focused section did not have the charges arranged in a straight line; instead, they were arranged in triangular shapes.
When three charges form a triangle, a calculation of the electrostatic force requires a two-dimensional vector treatment. This means that directions need to be expressed using either the polar method or the navigator method.
Read
Do “Example 10.5” on page 534 of your textbook. Be sure to follow the solution carefully.
Self-Check
Use this question to confirm your understanding of “Example 10.5.”
SC 7. Complete “Practice Problem” 2 on page 534 of your textbook.
Self-Check Answers
SC 7.
Given
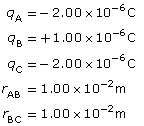
Required
to find the net force acting on sphere B, 
Analysis and Solution
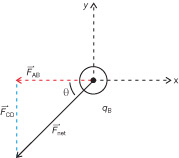
Step 1: Determine the direction of the forces.
The charge on sphere A is negative, and the charge on sphere B is positive. Therefore, the electrostatic force of qA on qB is an attractive force, pulling qB to the left. Similar thinking explains why the electrostatic force of qC on qB is an attractive force, pulling qB towards the bottom of the page.
If the polar method is used, then the following free-body diagram illustrates the forces acting on q2.
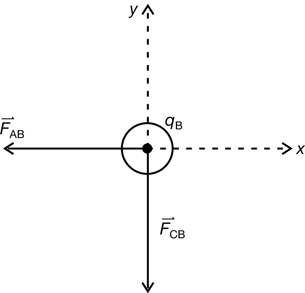
Note that since the spheres A and C have equal charges, and since these two spheres are the same distance from sphere B, is the same length as . This symmetry can be used to simplify the solution.
Step 2: Calculate the magnitude of the forces acting on sphere B.
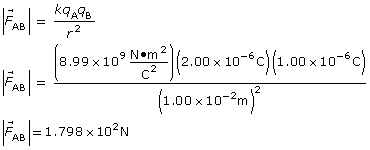
It is not necessary to do a separate calculation for the magnitude of since the calculation will be identical to that for . Therefore,
Step 3: Calculate the net electrostatic force on sphere B.
At this point, it is critical to realize that this equation is describing a two-dimensional vector addition. This means that the net force will be the resultant formed by adding and head to tail.
Since the net force is the hypotenuse of a right-angled triangle, the Pythagorean theorem can be used to find the magnitude of 
.
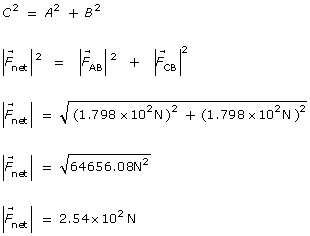
The fact that and have the same length means that the acute angle for must be 45°. Using the polar method, the direction of can be determined by measuring counterclockwise from the x-axis.
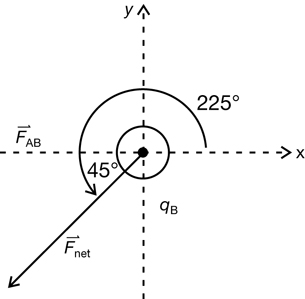
The direction of the net force is 225° using the polar method. If the navigator method were used, then south would replace the negative y direction and west would replace the negative x direction. The direction of the net force would be 45° south of west.
Paraphrase
The net electrostatic force acting on sphere B is 2.54 × 102 N [225°].
The previous example and practice problem show how powerful a systematic approach to problem solving can be. Did you recognize that this method of dealing with vectors using the polar or the navigator methods stemmed directly from your work with momentum earlier in the course? Even though the topic is no longer momentum, the same techniques work. This isn’t good luck—it is by design. Remember, the whole idea is to use the same overall strategies throughout the course so that you can become a successful problem solver.
As long as you take your time and consistently follow the recommended approach, even the most complicated problems can be solved. The key is to make effective use of diagrams—both vector diagrams and free-body diagrams.
Keep this in mind as you attempt the most complicated type of Coulomb’s law problem.
Open the multimedia learning object called Coulomb’s Law in 2D.
Read
Read “Example 10.6” on pages 535 to 537 of your textbook. Read the solution carefully. As you read, try to anticipate the next step in the solution.
Module 3: Lesson 3 Assignment
Remember to submit the answer to A 4 as part of your Module 3: Lesson 3 Assignment to your teacher for marks.
A 4. Do “Applications” question 24 on page 540 of your textbook.