Print this chapterPrint this chapter

Module 3

1. Module 3

1.24. Page 2

Module 3 Lesson 4

Module 3—Electrical Phenomena

 

Explore

 

Action at a Distance

 

Throughout this course, you have had many opportunities to observe electrostatic forces acting on charged objects. In many cases, the force was able to produce an observable effect even though the objects were not touching.

 

Two photos are shown side by side. The photo on the left shows a charged balloon attracted to a charged sweater. The photo on the right shows soap bubbles with an induced charge attracted to a charged Van de Graaff generator.

 

How were the positive charges on the sweater able to exert an electrostatic force on the negative charges on the balloon, even though the sweater was not touching the balloon? How was the negatively charged globe of the Van de Graaff generator able to exert forces on the soap bubbles, even though the Van de Graaff generator was not touching the bubbles?

 

field: a region of influence surrounding an object through which a force operates

These questions illustrate an important property of the electrostatic force: the force can act on a distant object without any apparent contact. This property has been called “action at a distance.” But naming this property is not the same as explaining it. After all, how does “action at a distance” work? What mechanism enables the electrostatic force to act through space? The answer to these riddles relates to an idea that you studied in previous courses—the concept of a field.

 

Read

 

You can learn more about how the concept of a field explains “action at a distance” by reading pages 542, 544, 545, and the bottom of page 546 of your textbook.

 

Self-Check

 

SC 1. Electrostatics is not the only branch of physics that utilizes the concept of a field.

  1. Identify another type of force that uses the field concept to explain “action at a distance.”

  2. Support your answer to the previous question by briefly describing an example of how the concept of a field is used to explain action at a distance for the force you identified.
Check your work.
Self-Check Answers

 

SC 1.

  1. The field concept is used to explain how the force of gravity is able to act across empty space to keep distant objects in orbit.

  2. This is one possible approach. As a space module approaches the moon, the path of the space module changes due to the influence of the moon’s gravitational force of attraction. Even though the moon is not touching the space capsule, the moon’s gravitational field acts upon the space capsule. The moon’s gravitational field is a property of the space around the moon that enables it to exert a gravitational force on the space capsule.

 

A photograph shot from space shows the Hubble Space Telescope orbiting Earth.

NASA

Reviewing Gravitational Fields

 

Before you begin your study of electric fields, you may find it helpful to review what you have learned about gravitational fields from previous courses. A satellite in orbit around Earth is a good example of gravitational fields at work.

 

The Hubble Space Telescope moves at about 8 km/s as it orbits about 600 km above Earth’s surface. It’s natural to wonder why an object moving so quickly, so far from the planet, stays in orbit. Shouldn’t this satellite just fly off into space?

 

Read

 

To answer this question, think about Earth’s gravitational field. If you need help remembering how Earth’s gravitational field acts on objects in orbit, read pages 200 and 201 of your textbook.

 

Self-Check

 

SC 2. Earth’s gravitational field can be described by a field diagram and by an equation.

  1. Describe the direction of Earth’s gravitational field.

  2. Although Earth’s gravitational field is invisible, it can be represented with a diagram showing gravitational field lines. Sketch a diagram representing Earth’s gravitational field. Use this diagram to compare the strength of Earth’s gravitational field at locations close to the planet and far from the planet.

  3. Compare the direction of the gravitational force of Earth acting on the Hubble Space Telescope to the direction of Earth’s gravitational field at the same location.

  4. Define gravitational field strength.

  5. State the equation for gravitational field. How does this equation support your answer to part c?

  6. Explain the difference between gravitational force and gravitational field.
Check your work.
Self-Check Answers

 

SC 2.

  1. Earth’s gravitational field is directed toward the centre of the planet.

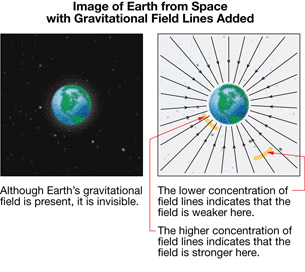
  2. The illustration on the left shows Earth. Although the gravitational field exists, it is invisible. The illustration on the right shows how Earth would look if the gravitational field could be seen.

  3. The gravitational force of Earth exerted on the Hubble Space Telescope is directed toward the centre of the planet. The gravitational field of Earth points in the same direction at this location.

  4. Gravitational field strength is defined as the gravitational force per unit mass at a specific location.

  5. The equation is

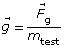
    This equation is a vector equation, with the gravitational field and the gravitational force pointing in the same direction.

  6. Gravitational force is the attractive force between any two objects due to their masses. The magnitude of the gravitational force can be experienced as a pull that can be measured with a spring scale calibrated in newtons.

    Gravitational field is the invisible region of influence that surrounds a source mass. The strength of the gravitational field is the ratio of the gravitational force per unit of test mass. The strength of the gravitational field can only be observed indirectly by observing the behavior of test bodies.

 

Equations for Gravitational Field

 

A vector equation emphasizes that the gravitational field and the gravitational force act in the same direction.

 

The illustration labels the key variables in the equation for gravitational field.

 

This equation provides a way to calculate the strength of the gravitational field in newtons per kilogram. Gravitational field strength can also be calculated in another way. Substituting Newton’s law of universal gravitation into the previous equation leads to an alternative equation that describes gravitational field strength.

 

The illustration labels the key variables in the longer equation for gravitational field.

 

Both equations for calculating the magnitude of the gravitational field for a point in space contain a mass variable, but these masses refer to different things.

 

The illustration labels the mass values in both equations for gravitational field.

 

Did You Know?

 

In Physics 20 you normally used m/s2 as the units for gravitational fields, which works very well for kinematics. In Physics 30 you will see N/kg, which is similar to the units for electric field strength of N/C.

 

Self-Check

 

How well do you remember gravitational fields? Try the Self-Check problems to review gravitational fields.

 

SC 3. Use the data from “Table 4.1” on page 218 of your textbook to calculate the gravitational field strength on the surfaces of Mars and Jupiter.

 

SC 4. An astronaut in her space suit has a mass of 105.5 kg. Use your answers from the previous question to determine the force of gravity that would act on this astronaut on the surface of each planet.

 

SC 5. Suppose a space probe moves from an initial position orbiting a planet to a final position that is only ¼ the distance away. Use the ratio method to determine how the value of gravitational field in the final position compares to the value of gravitational field in the initial position.

 

Check your work.
Self-Check Answer

 

SC 3.

 

Given

 

                

 

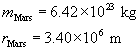
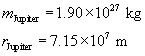
Required


The gravitational field strength at the surface of Mars.

The gravitational field strength at the surface of Jupiter.

 

Analysis

 

      

 

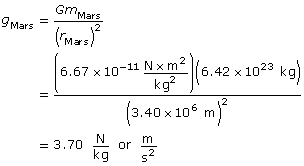
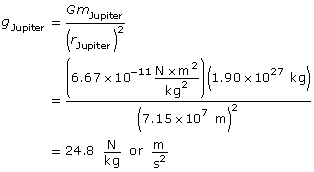
Paraphrase


The gravitational field strength on the surface of Mars is 3.70 N/kg.

The gravitational field strength on the surface of Jupiter is 24.8 N/kg.

 

SC 4.

 

Given

 

 

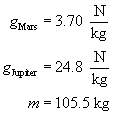
Required

 

The magnitude of the gravitational force acting on the astronaut on Mars and on Jupiter.

 

          

 

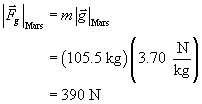
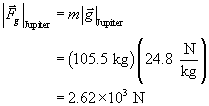
Paraphrase


The magnitude of the gravitational force acting on the astronaut on Mars is 390 N.

The magnitude of the gravitational force acting on the astronaut on Jupiter is 2.62 × 103 N.

 

SC 5.

 

 

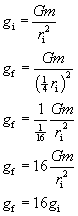
The new gravitational force is 16 times larger than the original force.