Module 3
1. Module 3
1.44. Page 4
Module 3—Electrical Phenomena
Lesson 6 Lab: Motion of Charges in Uniform Electric Fields
This lab consists of four parts. In Part A, you will examine the motion of a positively charged particle when it initially moves parallel to the electric field. In Part B you will examine the motion of a positively charged particle when it initially moves perpendicularly to the electric field. In Part C you will examine how a negatively charged particle will move when it starts parallel to the electric field. Finally, in Part D you will examine the motion of a negatively charged particle when it initially moves perpendicularly to the electric field.
Part A: Positive Particle Moves Parallel to the Electric Field
Purpose
In this part of the lab activity, you will use a computer simulation to collect data enabling you to answer the following questions:
- How does a positive particle move when the direction of its initial velocity is opposite to the direction of the electric field?
- How can this motion be explained using physics principles?
Procedure
Step 1: Open the Electric Field Potential simulation, and enter the following settings:
- Reset the simulation (
).
- Set the direction of the electric field to 0° W of S using the drop-down menu in the electric field display panel. Press the “enter” button on the keyboard to change the value in the textbox. Enter a value of 75 V/m for the magnitude of the electric field in the electric field display panel. Note that the electric field vector is shown as a large, green arrow. The small, green arrows indicate that the field has the same value at all locations on the screen.
- Set the direction of the initial velocity to 0° E of N using the drop-down menu in the velocity display panel. Enter a value of 150 m/s for the magnitude of the initial velocity in the velocity display panel. The velocity vector is shown as a magenta (purplish red) arrow.
- Set the particle's charge and mass to + 2.0 C and 3.0 kg, respectively.
- Drag the particle to a position low on the screen.
- Note that if you use “rewind” (
), you can return to these initial settings at any time during this lab activity. However, if you use “reset” (), you will have to re-enter all these initial settings.
If these settings have been applied, the screen should look like this:
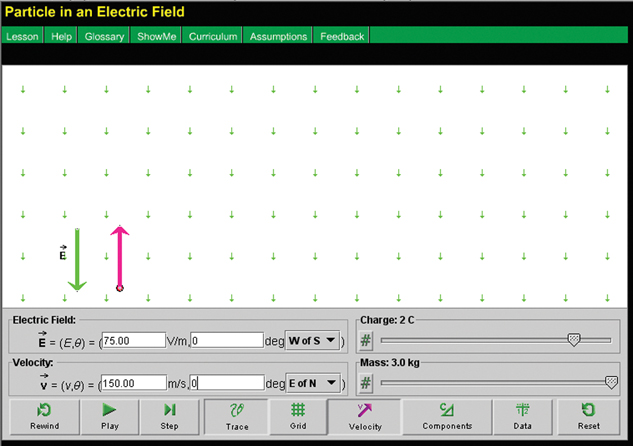
Step 2: Given these initial conditions, make a prediction as to how you think the particle will move if it is released. Press the “play” button (
) to confirm your prediction.
Step 3: Use “rewind” () to return to the initial settings. Repeat the previous step, but use “pause” (
) to stop the motion at the instant the particle reaches its highest point. Use “data” (
) to display information about the elapsed time, Δt, the x and y components of the acceleration (x, y), and the x and y components of the displacement (dx, dy) from the start of the motion.
Step 4: Collect the following data:
elapsed time Δt = ________ s
charge q = ____________ C
mass m = ___________ kg
Express the remaining values in terms of x and y components:
electric field 
= ___________V/m
acceleration (ax, ay) = ___________m/s2
initial velocity (vix, viy) = (0, 150) m/s
final velocity (vfx, vfy) = ____________m/s
maximum displacement (Δdx, Δdy) = __________m
Press the green button beside the 
once to see the final velocity in terms of x and y components.
final velocity (vfx, vfy) = ____________m/s
Note that the acceleration due to gravity is ignored in this simulation.
Analysis
Self-Check
Note that the values will be close to, but not necessarily exactly the same as, the answers shown. This is because you might have a slightly different time, ±0.20 s. However, your results will match the simulation’s values.
SC 7. Use Newton's laws of motion to verify the x and y components of the acceleration.
SC 8. Use calculations to verify the x and y components of the maximum displacement.
SC 9. Describe and explain a situation involving gravitational fields that could produce a similar type of motion.
Self-Check Answers
SC 7.
Given
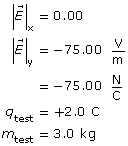
Required
The x and y components of the acceleration.
Analysis and Solution
- Newton’s second law states that an unbalanced force will cause a mass to accelerate in the direction of the force such that
.
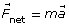- In this case the electrostatic force supplies the unbalanced force according to
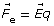. These equations can be combined to find the magnitude of the acceleration.
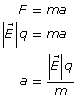
- Since the x and y components are independent of one another, the x and y components can be determined:
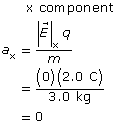
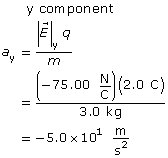
Paraphrase
In the x direction, the electric field is zero. Therefore, there is no force acting on the particle in the x direction and no acceleration. In the y direction, the electric field is 
, in the negative y direction. The resulting unbalanced force on the particle is also in the negative ydirection. These values are consistent with the values provided by the simulation, (0,−50.00) 
.
SC 8.
Given
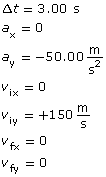
Required
The x and y components to the final displacement.
Analysis and Solution
In the x direction there is no motion since the velocity and acceleration values are all zero.
In the y direction the motion can be analyzed using a number of possible kinematics equations. One possible approach is shown here.
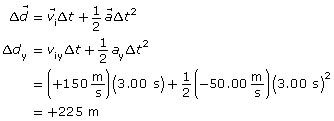
Paraphrase
The x and y components of the final displacement are (0, 225) m. These values are consistent with the values provided by the simulation (0, 225.1) m.
SC 9.
When a softball leaves a bat with an initial velocity directed straight up, the force of gravity acts to oppose the motion. Earth's gravitational field ensures that test bodies always experience a force of gravity directed downward—toward the centre of the planet.
According to Newton's second law, this downward force always causes an acceleration that is also directed downward—toward the centre of the planet. In terms of the motion of the ball, if it begins by moving straight up, it slows down, stops momentarily at the top of its path, and then speeds up as it returns to Earth.
Module 3: Lesson 6 Assignment
Remember to submit the answers to LAB 1 and LAB 2 to your teacher as part of your Module 3: Lesson 6 Assignment.
LAB 1. Summarize what you have learned from this simulation by stating what will happen when
- a positive particle has an initial velocity opposite to the direction of the electric field.
- a positive particle has an initial velocity in the same direction as the electric field.
LAB 2. Use physics principles to explain the motion you described in LAB 1.
Part B: Positive Particle Moves Perpendicular to the Electric Field
Purpose
In this part of the lab activity you will use a computer simulation to collect data enabling you to answer the following questions:
- How does a positive particle move when the direction of its initial velocity is perpendicular to the direction of the electric field?
- How can this motion be explained using physics principles?
Procedure
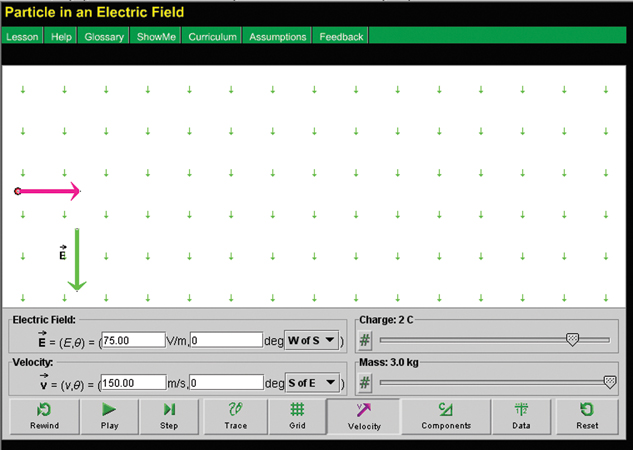
Step 1: Open the Electric Field Potential, Uniform simulation, and enter the following settings:
- Reset the simulation ().
- Set the direction of the electric field to 0o W of S using the drop-down menu in the electric field display panel. Enter a value of 75 V/m for the magnitude of the electric field in the electric field display panel.
- Set the direction of the initial velocity to 0o S of E using the drop-down menu in the velocity display panel. Enter a value of 150 m/s for the magnitude of the initial velocity in the velocity display panel.
- Set the particle's charge and mass to +2.0 C and 3.0 kg, respectively.
- Drag the particle to a position on the left of the screen and centred vertically.
- Note that if you use “rewind” (), you can return to these initial settings at any time during this lab activity. However, if you use “reset” (), you will have to re-enter all these initial settings.
If these settings have been applied, the screen should look like this.
Step 2: Given these initial conditions, make a prediction as to how you think the particle will move if it is released. Press the “play” button () to confirm your prediction. To see the path that the particle followed, use the “rewind” button (). Then use the “trace” button (
).
Step 3: Use “rewind” () to return to the initial settings. Repeat the previous step, but use “pause” () to stop the motion at the instant the particle starts to leave the display. Use “data” (
) to display information describing the particle in this location.
Step 4: Collect the following data:
elapsed time
charge
mass
Δt = ________s
q = ____________C
m = ___________kg
Express the remaining values in terms of x and y components:
electric field
acceleration
initial velocity
final velocity
displacement
= ___________V/m
(ax, ay) =___________m/s2
(vix, viy) = (150, 0) m/s
(vfx, vfy) = ____________m/s
(Δdx, Δdy) = __________m
Note that the acceleration due to gravity is ignored in this simulation.
Analysis
Self-Check
SC 10.
- Use calculations to verify the x component of the displacement.
- Use calculations to verify the y component of the displacement.
SC 11. Use calculations to verify the y component of the final velocity.
SC 12. Use calculations to verify the magnitude and the angle of the final velocity as displayed in the velocity display panel.
SC 13. Describe a situation involving gravitational fields that could produce a similar type of motion.
Self-Check Answers
Your answers may be slightly different due to different time values. However, your answers will match the simulation.
SC10.
a.
Given
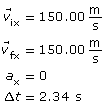
Required
The x component of the displacement.
Analysis and Solution
Since there is no x component of the electric field, there is no electrostatic force acting in the x direction. Therefore there is no acceleration in the x direction. In other words, the charge moves with uniform motion in the x direction.
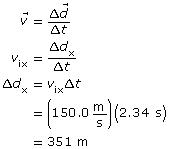
Paraphrase
The x-component of the displacement is calculated to be 351 m. This matches the value provided by the simulation.
SC10.
b.
Given
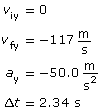
Required
The y component of the displacement.
Analysis and Solution
Since the y component of the electric field is in the negative y direction, the positive particle experiences an electrostatic force in the negative y direction. Since this electrostatic force is unbalance, the positive particle accelerates uniformly in the negative y direction.
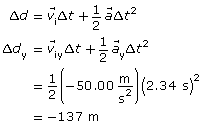
Note: in step 3, viy = 0 so the entire term is zero and is dropped for simplicity.
Paraphrase
The y component of the displacement is −137 m. This matches the value provided by the simulation.
SC11.
Given
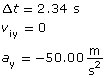
Required
The y component of the final velocity
Analysis and Solution
Since the y component of the electric field is in the negative y direction, the particle experiences an electrostatic force in the negative y direction. Since this electrostatic force is unbalanced, the positive particle accelerates uniformly in the negative y direction.
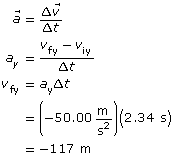
Note: in step 3, viy = 0 so it is dropped for simplicity.
Paraphrase
The y component of the final velocity of the particle is calculated to be −117 m/s. This matches the value provided by the simulation.
SC12.
Given
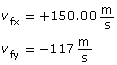
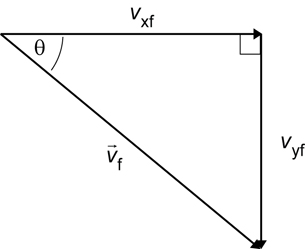
Required
The magnitude and the direction of the final velocity.
Analysis and Solution
The magnitude of the velocity can be found using the Pythagorean theorem. The direction can be found using trigonometry.
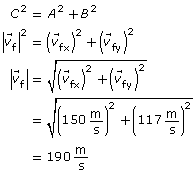
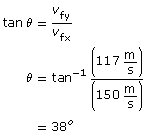
Paraphrase
The final velocity is calculated to be 190 m/s [38° S of E]. This matches the value provided by the simulation.
SC 13. A similar type of motion could be produced if an object were launched horizontally from the edge of a cliff. The initial velocity would be at a right angle to the gravitational field, so if the effects of air resistance could be ignored, the object would maintain its velocity in the horizontal direction while accelerating in the vertical direction. The resulting path would be the characteristic parabola of projectile motion.
Module 3: Lesson 6 Assignment
Remember to submit the answers to LAB 3 and LAB 4 to your teacher as part of your Module 3: Lesson 6 Assignment.
LAB 3. Describe the motion of a positive particle when the direction of its initial velocity is perpendicular to the direction of the electric field.
LAB 4. Use physics principles to explain the motion you described in LAB 3.
Part C: Negative Particle Moves Perpendicular to the Electric Field
Purpose
In this part of the lab activity you will use a computer simulation to collect data enabling you to answer the following question:
- How does a negative particle move when the direction of its initial velocity is perpendicular to the direction of the electric field?
- How can this motion be explained using physics principles?
Procedure
Step 1: If you still have the simulation open from Part B of this lab activity, continue with the next step. Otherwise, re-open the Electric Field Potential, Uniform simulation, and enter the settings described in Step 1 of Part B.
Step 2: To return the particle to its initial position, press “rewind” ().
Step 3: Make the following adjustments to the initial settings:
- Change the charge of the particle to –2.0 C.
- Set the direction of the initial velocity to 0o N of E using the drop-down menu in the velocity display panel. Enter a value of 150 m/s for the magnitude of the initial velocity in the velocity display panel.
If these settings have been properly applied, the screen should look like this:
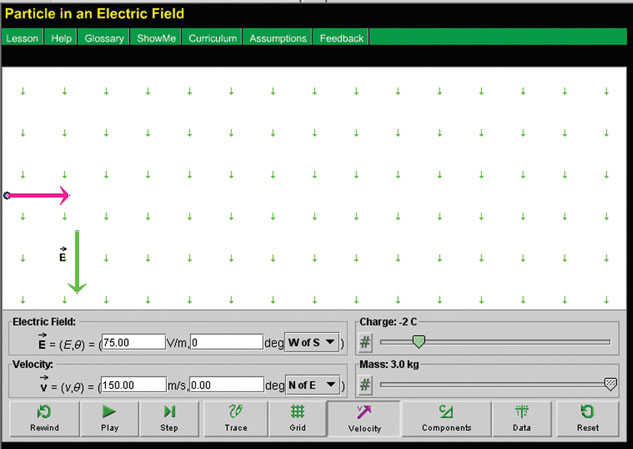
Step 4: Given these initial conditions, predict how the particle will move if it is released. Press the “play” button () to confirm your prediction.
Step 5: Use “rewind” () to return to the initial settings. Repeat the previous step, but use “pause” () to stop the motion at the instant the particle starts to leave the display. Use “data” () to display information describing the particle at this location.
Step 6: Collect the following data:
elapsed time
charge
mass
Δt = ________s
q = ____________C
m = ___________kg
Express the remaining values in terms of x and y components:
electric field
acceleration
initial velocity
final velocity
displacement
= ____________V/m
(ax, ay) =_____________m/s2
(vix, viy) = (150, 0) m/s
(Δdx, Δdy) = __________m
(vfx, vfy) = ____________m/s
Note that the acceleration due to gravity is ignored in this simulation.
Analysis
Self-Check
SC 14. a. Use calculations to verify the x component of the displacement.
- Use calculations to verify the y component of the displacement.
SC 15. Use calculations to verify the y components of the final velocity.
SC 16. Use calculations to verify the magnitude and direction of the final velocity as displayed in the velocity display panel.
SC 17. In this part of the lab, a particle that had an initial velocity perpendicular to a field moved through a parabolic trajectory so that it accelerated in a direction opposite to the external field. Explain why this situation could never happen in a gravitational field.
Self-Check Answers
SC 14.
a.
Given
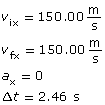
Required
The x component of the displacement.
Analysis and Solution
Since there is no x component of the electric field, there is no electrostatic force acting in the x direction. In other words the charge moves with uniform motion in the x direction.
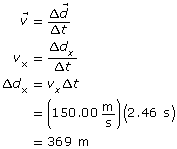
Paraphrase
The x component of the displacement is calculated as 369 m, which matches the value provided by the simulation.
b.
Given
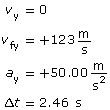
Required
The y component of the displacement.
Analysis and Solution
Since the y component of the electric field is in the negative y direction, the particle experiences an electrostatic force in the positive y direction. This is because the charge is negative and experiences a force opposite to the direction of the electric field. Since the electrostatic force is unbalanced, the negative particle accelerates in the positive y direction.
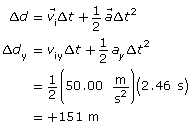
Paraphrase
The y component of the displacement is calculated as +151 m, which matches the value provided by the simulation.
SC 15.
Given
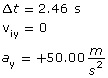
Required
The y component of the final velocity
Analysis and Solution
The y component of the electric field is in the negative y direction. However because the particle is negative, it experiences a force in the positive y direction. (See SC 14.b. for explanation) The electrostatic force in the positive y direction is unbalanced, so the negative particle accelerates in the positive y direction.
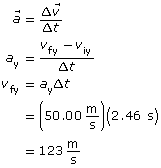
Paraphrase
The y component of the final velocity is calculated to be 123 m/s. This matches the value provided by the simulation.
SC 16.
Given
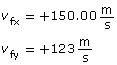
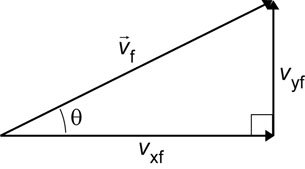
Required
The magnitude and direction of the final velocity.
Analysis and Solution
The magnitude of the velocity can be found by using the Pythagorean theorem. The direction can be found by using trigonometry.
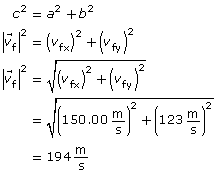
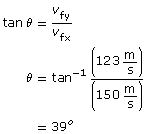
Paraphrase
The final velocity is calculated to be 194 m/s [39o N of E], which matches the value provided by the simulation.
SC 17. There are two types of test bodies that can be accelerated in electric fields: positively charged test bodies and negatively charged test bodies. Positively charged particles accelerate in the same direction as the electric field, and negatively charged particles accelerate opposite to the direction of the field.
However, in gravitational fields there is only one kind of test body: an object with mass. Objects with mass always accelerate in the same direction as the gravitational field. So it is impossible for a test mass to be injected at right angles to a gravitational field and then accelerate in a direction that is opposite to that of the field.
Module 3: Lesson 6 Assignment
Remember to submit the answers to LAB 5 and LAB 6 to your teacher as part of your Module 3: Lesson 6 Assignment.
LAB 5. Describe the motion of a negatively charged particle when the direction of its initial velocity is perpendicular to the direction of the electric field.
LAB 6. Use physics principles to explain the motion you described in LAB 5.
Part D: Producing an Un-deflected Path Through an Electric Field
Purpose
In this part of the lab activity you will use a computer simulation to collect data enabling you to answer the following question:
- If a particle is given an initial velocity perpendicular to an electric field, under what circumstance could this particle move un-deflected with uniform motion through the electric field? Assume the electric field is the only field present.
Procedure
Step 1: If you still have the simulation open from this lab activity, continue with the next step. Otherwise, re-open the Electric Field Potential, Uniform simulation, and enter the settings described in Step 1 of Part B.
Step 2: To return the particle to its initial position, press “rewind” ().
Step 3: Without changing the settings for the electric field or the velocity, what adjustment could you make so that the particle moves with only uniform motion when you release the particle? Make the necessary adjustment and press “play” () to confirm your prediction.
Step 4: Use “rewind” () to return to the initial settings. Repeat the previous step, but use “pause” () to stop the motion at the instant the particle starts to leave the display. Use “data” () to display information describing the particle in this location.
Self-Check
SC 18. Identify the values on the data chart that confirm that the particle is only moving with uniform motion.
Self-Check Answer
SC 18. One set of values that confirm that the particle is only moving with uniform motion are the values for acceleration. Both the x and y components of the acceleration are zero.
Module 3: Lesson 6 Assignment
Remember to submit the answer to LAB 7 to your teacher as part of your Module 3: Lesson 6 Assignment.
LAB 7. Explain the circumstances that enable an article to move un-deflected with uniform motion through an electric field if it is given an initial velocity perpendicular to the electric field. Assume the electric field is the only field present.