Module 4

Module 4—Magnetic and Electric Fields in Nature and Technology

 

Read

 

See “Charged Particle Motion in a Magnetic Field” on pages 596−597 of the textbook for further explanation and illustrations of the magnetic force.

 

Try This—Part 2: The Force Exerted by a Magnetic Field on a Charged Particle

 

Problem

 

On what physical quantities does the force exerted on a particle in a magnetic field depend, and how does it depend on these quantities?

 

Background Information

 

The simulation in Part 1 of this Try This activity can be used to determine the relationship between the magnetic force and the following quantities:

• (m) mass of the particle
  

• (q) charge of the particle
  

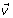• () velocity of the particle
  

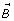• () magnetic field strength

To establish a relationship between the magnetic force and any one variable (the responding variable), you would change one variable at a time (the manipulated variable) and observe any resulting changes in the magnetic force. With all other variables held constant, a change in one variable and a corresponding change in the magnetic force would indicate a relationship. The amount of change would further indicate the nature of the relationship.

 

In order to test the relationship between the magnetic forces and each of the four quantities listed above, there needs to be a way of measuring the force. Newton's second law provides such a way.

 

Newton's Second Law     F = ma        (1)

 

 

In uniform circular motion, the magnitude of the acceleration a is equal to equation (2), where r is the radius of the circular orbit and v the particle's constant speed.

 

 

Substituting equation (2) into equation (1) gives a measure of the magnitude of the magnetic force.

The simulation displays the value of r. In the laboratory, you would be able to measure r and manipulate the values of m and v. Therefore, you can measure the magnetic force by determining the value of the right side of equation (3).

 

The nature of the relationship is further revealed by graphing the effect of the changing variable on the magnetic force (the force is determined based on equation (3), using the radius of the particles’ path in the magnetic field). The shape of the following reference graphs reveals the relationship between two variables.

 

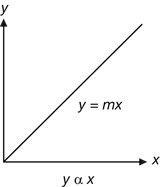
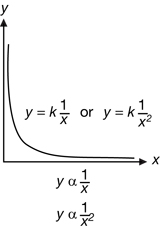
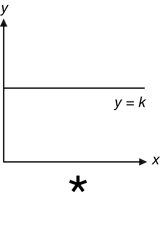
*The horizontal line indicates that the function is a constant. In this specific case the relationship is that mass does not affect the magnitude of the magnetic force.

 

Procedure

1. Open the simulation of a Particle in a Magnetic Field.
   
   

2. On the simulation, set the mass, speed, charge, and magnetic field strength as follows:
   
   m = 1.0
   v = 150
   q = 1.0
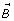   = magnitude 100, direction out of screen
   
   

3. Play the simulation and record the value of r in Table 1. Press the data button to display the radius and period of motion.
   
   

4. Using equation (3), 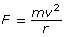, calculate the magnitude of the magnetic force based on the radius. Add this value to Table 1.
   
   

5. On the simulation, click “rewind” (), and double the mass (m = 2). Make no other changes.
   
   

6. Play the simulation and record the value for the radius of the path (r).
   
   

7. Calculate the magnetic force again.
   
   

8. Complete Table 1 by sequentially changing the value of the mass and recording the new radius and magnetic force.
   
   

9. Repeat steps 2 to 8 to complete the remaining data tables for the effects of velocity, charge, and magnetic field strength on the magnitude of the magnetic force. Vary only one variable at a time.

Observations

Table 1: How Mass Affects Force

Mass of Particle (m)	Radius of Path (r)	Magnetic Force from Equation (3) (Fm)
1
2
3

 

Table 2: How Speed Affects Force

Speed of Particle (v)	Radius of Path (r)	Magnetic Fforce from Equation (3) (Fm)
150
200
250
300

 

Table 3: How Charge Affects Force

Charge (q)	Radius of Path (r)	Magnetic Force from Equation (3) (Fm)
1
2
3

 

Table 4: How Magnetic Field Strength Affects Force

Magnetic Field Strength (B)	Radius of Path (r)	Magnetic Force from Equation (3) (Fm)
100
150
200
250
300

 

Analysis

1. Graph each variable versus the magnetic force. The manipulated variable is on the x-axis and the responding variable (the magnetic force) is plotted on the y-axis. Label each graph and draw the line of best fit. Alternatively, you may choose to build your graphs in Excel and insert them.
   
   

2. According to the mass versus magnetic force graph, is the magnetic force affected by the mass of the charged particle? State the mathematical relationship.
   
   

3. According to the speed versus magnetic force graph, is the magnetic force affected by the speed of the charged particle? State the mathematical relationship. 
   
   

4. According to the charge versus magnetic force graph, is the magnetic force affected by the charge of the charged particle? State the mathematical relationship.
   
   

5. According to the magnetic field versus magnetic force graph, is the magnetic force affected by the strength of the magnetic field in which the particle travels? State the mathematical relationship. 
   
   

6. Combine the results of questions 2 to 5 to produce an equation that describes the magnetic force in terms of the particle’s charge, velocity, and the strength of the external magnetic field that it moves in.

7. Manipulate your equation from question 6 to isolate for the term for the magnetic field (B). What is one way to express the units of the tesla? You will revisit these units in Lesson 3 in relation to the definition of current.

Save your completed observation tables and responses to all Analysis questions in your course folder.

 

 

Can you see that the following five quantities are equivalent?

 

 

Note: In 1948 the Bureau International des Poids et Mesures decided that the ampere is a base unit and not the coulomb.

Physics 30 Learn EveryWare © 2009 Alberta Education