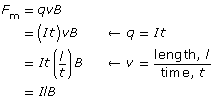Module 4

1. Module 4

1.17. Page 2

Lesson 3

Module 4—Magnetic and Electric Fields in Nature and Technology

Explore

A photograph shows a multimeter, which can measure the current, or amount of charge per second, flowing through a conductor.

What is an electric current? In earlier science courses you learned that an electric current is defined by the collective movement of many, many charges. The photograph to the right shows a multi-meter, a device for displaying data related to electric current and voltage in a variety of ways. Many charges make up the electric current that flows through it. The current, or amount of charge that flows past a fixed point in a one-second interval, is displayed in amperes (A). The unit of electric current is named for André-Marie Ampère (1775–1836), a French scientist who contributed extensively to our understanding of the relationship between current and magnetic force.

electric current: the amount of charge, in coulombs, that passes a fixed point in a conductor in a one-second interval

Electric current expressed as an equation is as follows:

Quantity	Symbol	SI Unit
electric current	I	ampere (A)
charge of the particle	q	coulombs (C)
interval	t	seconds (s)

The SI unit of electric current is the ampere (A). One ampere of current is equivalent to one coulomb of charge passing a fixed point in a conductor in a one-second interval, 1 A = 1 C/s.

Read

Read “Electric Current” on page 602 of the textbook.

Try This

TR 1.

Complete “Practice Problems” 1 and 2 on page 603 of the textbook.
In “Practice Problem” 2, how many electrons would have passed through the appliance in the 10-second interval?

Module 4: Lesson 3 Assignment

Remember to submit the answers to A 1 to your teacher as part of your Module 4: Lesson 3 Assignment.

A 1. A compact fluorescent light bulb draws a current of 0.10 A for one hour.

How much charge flows through the bulb in one hour?
How many electrons flow through the light bulb in the hour? Remember the charge of one electron is the elementary charge on your physics data sheet.

Magnetic Force Direction

Recall from Lesson 2 that a moving charge induces a magnetic field and that when this magnetic field encounters an external magnetic field, the two fields will interact and cause the moving charge to experience a magnetic force (both magnitude and direction).

The hand rule used to predict the direction of the magnetic force acting on a charged particle in Lesson 2 can be used in a similar way to predict the direction of magnetic force acting on a current-carrying wire.

Watch and Listen

Complete the tutorial Force on a Wire. It demonstrates how the hand rule is applied to determine the direction of the magnetic force that acts on a perpendicular current-carrying conductor in a magnetic field.

Left-hand Rule for Magnetic Force

The direction of the force exerted on a current-carrying conductor perpendicular to a magnetic field can be visualized by means of the left-hand rule illustrated in Figure 1. (There are several hand rules for this purpose. The following is only one suggestion.)

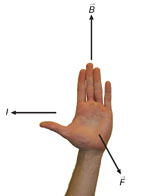
A labelled illustration of the left hand shows the left hand rule. The view shows the hand held vertically with the palm facing the viewer, thumb to the left and fingers pointing straight up. The thumb points in the direction of the current, the fingers point in the direction of the magnetic field and the palm points in the direction of the magnetic force.

Figure 1

Hold your left hand flat with outstretched fingers in the direction of the magnetic field () and with the thumb pointing off to one side in the direction of the negative current flow. The palm of your hand will then be pointing in the direction of the magnetic force () that acts on the conductor.

Read

Read “Left-hand Rule for Magnetic Force” on page 604 of the textbook for a summary of this hand rule. To further your understanding, view the animation Left-hand Rule for Magnetic Force.

Magnetic Force Magnitude

By combining the equation that describes the magnetic force acting on a moving, charged particle with the definition of electric current, it is possible to determine the size of the magnetic force acting on a current-carrying conductor (assuming the current direction is perpendicular to the magnetic field).

magnetic force on a

charged particle

current

Combining both equations and treating the velocity in terms of units gives an equation that describes the size of the magnetic force acting on a current (I) carrying conductor of specific length (l), which is perpendicular to a magnetic field (B).

Expressed as an equation, .

Magnetic Force: The deflecting magnetic force acting on a current-carrying conductor is proportional to the product of the conductor’s length in the field and the current it carries perpendicular to the magnetic field at its location.

Expressed as an equation,

Quantity	Symbol	SI Unit
magnetic force	F	newton (N)
current	I	ampere (A)
length of conductor	l	metres (m)
strength of the magnetic field	B	tesla (T)

In cases where only a component of the current and/or magnetic field are perpendicular, only the components that are perpendicular are used to calculate the size of the magnetic force.

Example Problem 1.

Determine the magnitude and direction of the magnetic force acting on a 0.500 m long conductor that carries a 2.00 A e– flow current west through a 3.50 × 10–1 T magnetic field that is directed north.

Given

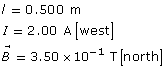
Magnitude

Fm = IlB
Fm = (2.00 A)(0.500 m)(3.50 × 10–1 T)
Fm = 3.50 × 10–1 N

Direction

According to the left-hand rule for negative charges, the force is upward.

Paraphrase

The magnetic force acting on the wire is 3.50 × 10–1 N [up].