Module 5
1. Module 5
1.19. Page 2
Module 5—Wave Theory of Light
 Explore
Explore

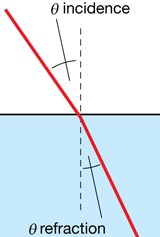
Refraction is a change in the direction of a light wave caused by a change in its speed as the light wave passes at an angle from one medium to the next. In the ray diagram example, a light ray is incident on the surface of water. Some of the light is reflected and some of the light slows down as it enters the water and is refracted.
According to the law of reflection, the angle of reflection is identical to the angle of incidence.
The angle of refraction, however, is not the same as the angle of incidence. It is determined by Snell’s Law. The simplest way to write Snell’s Law is as follows:
![]() , where n is the index of refraction
, where n is the index of refraction
The simple form of Snell’s Law assumes that the medium the light is leaving is air. The refractive index of air is 1.0003, which is close to, and usually assumed to be the same as, the refractive index of a vacuum (n = 1.000). This is true because the speed of light in air is nearly identical to its speed in a vacuum so, as it passes from air into a vacuum, it is only refracted by a very small amount, making the ratio of the ![]() equal to 1. The amount of refraction in other materials, as light enters them from air or a vacuum, is much more and leads to higher indexes of refraction. Therefore, the index of refraction is a relative measure of how much the light changes speed and is bent as it moves between two mediums.
equal to 1. The amount of refraction in other materials, as light enters them from air or a vacuum, is much more and leads to higher indexes of refraction. Therefore, the index of refraction is a relative measure of how much the light changes speed and is bent as it moves between two mediums.
refraction: a change in the direction of a wave due to a change in its speed
Snell’s Law: for any angle of incidence greater than zero, the ratio of
![]()
refractive index: a ratio comparing the speed of light in a vacuum to its speed in a given medium
Table 1: Absolute Refractive Indexes of Some Common Materials
| Medium | Index of Refraction |
vacuum |
1.0000 |
air |
1.0003 |
ice |
1.31 |
water |
1.33 |
quartz glass |
1.47 |
crown glass |
1.52 |
lucite (plexiglass) |
1.52 |
diamond |
2.42 |
 Try This
Try This
TR 1. Based on Table 1, in which medium is light most refracted as it enters the medium from air?
A useful rule of thumb to remember concerns how light bends as it either enters a region of increased refractive index or vice versa. You can discover this rule using this Light Refraction simulation.
Once the simulation is open, do the following:
- Click the “Add” button (
 ). This will add a second medium to the display window (medium 1 and medium 2), both with a refractive index (n) = 1.0.
). This will add a second medium to the display window (medium 1 and medium 2), both with a refractive index (n) = 1.0.
- Double-click anywhere in the bottom layer and enter the refractive index (n) of water 1.33.
- Click and drag the laser into the top layer. Next, click the tip of the laser and point it down into the water layer. Vary the angle of the beam by adjusting the laser’s direction. Note the way in which the light bends as it enters the denser (water) layer. (Toward or away from the normal?)
- Move the laser pointer to the water layer and point it upward into the air layer. Vary the angle and note the way in which the light bends as it enters the rarer (air) layer. (Toward or away from the normal?)
 Module 5: Lesson 4 Assignment
Module 5: Lesson 4 Assignment
Remember to submit your answers to LAB 1 to your teacher as part of your Module 5: Lesson 4 Assignment.
LAB 1. Use the Light Refraction simulation to determine the answer to the following two questions:
- When light travels from a low-index medium (fast) into a high-index medium (slower), does the ray bend toward or away from the normal?
- When light travels from a high-index (slower) medium into a low-index (fast) medium, does the light ray bend toward or away from the normal?
 Self-Check
Self-Check
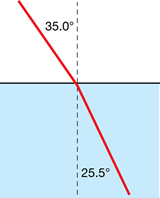
SC 1. A laser is directed into a pool of water (nwater = 1.33). The beam contacts the air-water interface with an angle of incidence equal to 35.0°. Using the simple form of Snell’s Law, calculate the angle of refraction (relative to the normal) with which it travels through the water. Show your calculations and label the ray diagram showing the angle of incidence and angle of refraction. Verify your answer using the Light Refraction simulation.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Given
![]()
Required
the angle of refraction, n2
Analysis and Solution
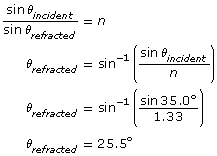
Paraphrase
The angle of refraction is 25.5°.
A More General Form of Snell’s Law
The general form of Snell’s Law is used to describe the change in direction of light when it moves between any two media and not just out of air. The Light Rerfraction simulation will be used to determine the general form of Snell’s Law.
 Module 5: Lesson 4 Assignment
Module 5: Lesson 4 Assignment
Remember to submit your answer to LAB 2 to your teacher as part of your Module 5: Lesson 4 Assignment.
LAB 2. Set up the Light Refraction simulation with two refractive layers. You will need to vary the refractive index for each layer and the angle of the light ray in order to complete Table 2. Select "Show Calcs" (![]() ) to assist in recording angles. Get as close to the θin as you can, but record the actual value that you use.
) to assist in recording angles. Get as close to the θin as you can, but record the actual value that you use.
Table 2: Refraction Data
| n1 | θin |
n1sinθin |
n2 |
θout |
n2sinθout |
1.20 |
45° |
|
1.40 |
|
|
1.30 |
32° |
|
1.66 |
|
|
1.45 |
45° |
|
1.23 |
|
|
1.51 |
40° |
|
1.00 |
|
|
1.65 |
45° |
|
1.80 |
|
|
According to your data in Table 2, which two values are always equal to one another?
Snell’s Law: The general form of Snell’s Law relates the ratio of the indexes of refraction to the ratio of the sine of the angles of incidence and refraction.
Expressed as an equation,
![]()
| Quantity | Symbol | SI Unit |
| refractive index of the first medium | n1 | coefficient (no units) |
| refractive index of the second medium | n2 | coefficient (no units) |
| angle of incident (measured from the normal) | θ1 | degrees |
| angle of refraction (measured from the normal) | θ2 | degrees |
 Try This
Try This
TR 2. Snell’s Law may also be written as n1sinθ1 = n2sinθ2. Does the data collected in Table 2 support the general form of Snell’s Law? Explain and provide two sample calculations to support your explanation.
 Self-Check
Self-Check
SC 2. A laser is submerged in oil (noil = 1.48) and directed into a pool of water (nwater = 1.33) with an angle of incidence equal to 35.0°. Calculate the angle of refraction. Show your calculations and use the Light Refraction simulation to verify your answer.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 2.
Given
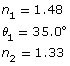
Required
the angle of refraction, θ2
Analysis and Solution
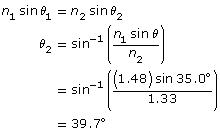
Paraphrase
The angle of refraction is 39.7°.
 Try This
Try This
TR 3. Complete “Practice Problems" 1–4 on page 668 of your textbook.
Snell’s Law can be expanded when you consider light as a transverse wave. In the expanded form, frequency, wavelength, and speed are related according to the following equation:
![]()
 Read
Read
Read “Snell’s Law, Refraction, and Wavelength” on pages 669–670 for a derivation of this equation based on the transverse wave model of EMR.
 Try This
Try This
TR 4. Complete “Practice Problems” 1(a), 1(b), 2, and 3 on page 670 of your textbook. Note: Index of refraction values are given on page 667.