Print this chapterPrint this chapter

Module 5

1. Module 5

1.22. Page 5

Lesson 4

Module 5—Wave Theory of Light

 

A photo shows a double rainbow arcing over a stand of trees. A rainbow is an optical illusion produced by the refraction of sunlight in water droplets in Earth’s atmosphere.

© Tad Denson/shutterstock

Reflect and Connect

 

Seen here is a double rainbow, a fantastic, natural demonstration of refraction resulting in the dispersion of white light. This rainbow appears to be very close to the photographer, compliments of the light rain and mist coming from above. The illusion is produced when sunlight is incident on water droplets in the atmosphere.

 

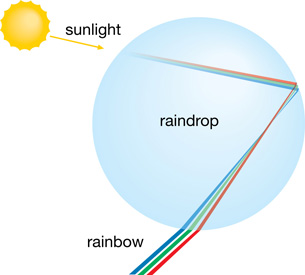
A diagram shows sunlight refracted as it enters a raindrop and exits to produce a spectrum of colours.

The various wavelengths of visible light in sunlight are refracted as they enter the raindrop. Each wavelength is reflected at the back of the droplet reversing the order of the spectrum as it passes through an internal focal point before being refracted a second time when it emerges. If this process occurs in many water droplets simultaneously, the optical illusion of a rainbow can be observed. The illusion only appears to exist at a particular location in the sky or land, but this position depends on the position of the Sun, water, and observer. As the observer moves, the rainbow moves with the observer, so you will never get to the end of a rainbow to recover a pot of gold!

 

Reflect on the Big Picture

 

Do refraction, total internal reflection, and dispersion support the wave model of light? The bending or refracting of light can be understood in terms of a transverse wave. Recall that the universal wave equation relates the speed, wavelength, and frequency of a transverse wave:

 

v = fλ

 

Consider a transverse light wave travelling from air into water. As the light wave enters the water, it slows down and the wavelength gets compressed. The frequency, however, remains unchanged, since the waves do not pile up at the boundary. The number of waves arriving at the boundary each second is equal to the number of waves leaving the boundary every second. Therefore, the frequency of the wave is constant as the wavelength shrinks. This helps us understand the change in speed when EMR is considered as a transverse wave. If the wavelength shrinks and the frequency remains constant, then the speed must also be reduced according to the universal wave equation.

 

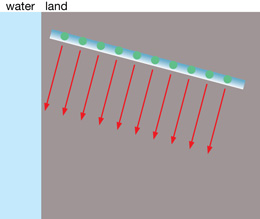
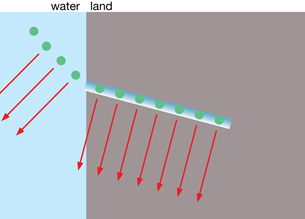
As the wave fronts are compressed and slowed in the water, they change direction relative to the arriving, uncompressed, faster wave fronts still in the air. To visualize this in terms of wave fronts, imagine a line of 100 people all holding hands and running on the beach. If those runners closest to the water enter it and slow down, what happens to the shape of the line?

 

Two diagrams represent a line of connected people running from land into water at an angle. In the first diagram, the line of people is on land; in the second, the people closest to the water have run into the water and changed the shape of the line, bending it. This is analogous to a transverse wavefront bending as it moves from a low index medium to a high index medium.
Two diagrams represent a line of connected people running from land into water at an angle. In the first diagram, the line of people is on land; in the second, the people closest to the water have run into the water and changed the shape of the line, bending it. This is analogous to a transverse wavefront bending as it moves from a low index medium to a high index medium.

 


Module 5: Lesson 4 Assignment

 

Remember to submit the Module 5: Lesson 4 Assignment to your teacher.