Module 6

1. Module 6

1.9. Page 3

Lesson 2

Module 6—Wave-Particle Duality and Quantum Physics

The Photoelectric Effect and Quantum Theory

work function: the minimum energy that a photon can have to cause photoemission from a metal

Each metal has a specific work function.

Einstein explained the general observations for the photoelectric effect in 1905 using Planck’s quantum hypothesis. He proposed that the energy delivered by a single incident photon is defined by Ephoton = hf and that a certain amount of energy, called the work function, is required to free an electron from a metal surface. For example, it takes 4.70 eV of energy to eject an electron from copper, but only 2.30 eV of energy is required to free an electron from potassium. The work function (W) is related to the threshold frequency by Planck’s equation, W = hfo. Notice that in Graph 3 on the previous page the threshold frequency for both copper and potassium supports this idea. Copper has a higher threshold frequency than potassium since it requires more energy to free an electron. This means that when a photon with energy greater than that of a metal’s work function is incident on the surface, a photoelectron will be emitted.

Einstein’s theory also predicted that if an incident photon has more energy than the metal’s work function, the ejected photoelectron would leave with some kinetic energy, thus supporting the law of conservation of energy.

Watch and Listen

This is a screen capture of the multimedia piece you will complete in SIM 1.

Experiments performed by Robert Millikan in 1916 provided the evidence to support Einstein’s photoelectric theory. A simulation will be used to explore a simplified version of this work.

SIM 1. Open the photoelectric effect simulation1 and adjust the intensity slider ( A screenshot of the simulation shows the setting of the intensity slider. ) to 100% and select the () graph mode. With the graph showing, slide the intensity slider to 0% and back again to 100%. Does the observed graph match Graph 1 on the previous page? Explain this relationship and what “intensity” means in a quantum context.

A screenshot of the simulation shows the equipment set-up used by Einstein.

1© The University of Colorado, under the GNU General Public License (GPL)

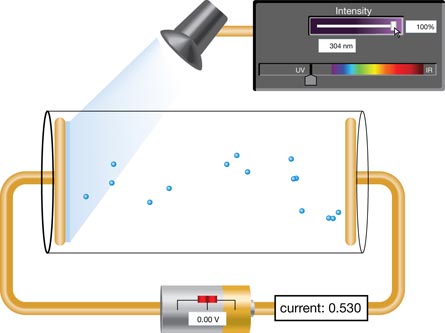
In this simplification of Millikan’s experiment, photons above the threshold frequency strike a metal plate in an evacuated tube. A positive electrode connected to a power supply collects the emitted photoelectrons, thus establishing a photoelectric current.

When the power supply polarity is reversed, it produces an electric force that effectively repels the photoelectrons and slows the current. At sufficient voltage—called the stopping voltage or stopping potential difference—the photoelectric current observed in the ammeter drops to zero.

stopping voltage: the potential difference for which the kinetic energy of a photoelectron equals the work needed to move through a potential difference, V

SIM 2. With the intensity at 100% and the wavelength in the UV range, many photoelectrons contribute to the current in the circuit displayed in the yellow box. Click and drag the voltage slider on the battery ( A screenshot of the simulation shows the stopping voltage setting. ) to adjust the electric field in the tube. Observe the charge on each electrode. What happens to the motion of the photoelectrons? Explain why this happens.

SIM 3. Set the photon wavelength to 298 nm and the intensity to 100%. Using the battery slider, determine the minimum voltage that brings the current to zero amps.

Vstop = __________________

Now change the intensity to 50%. Using the battery slider, determine the minimum voltage that brings the current to zero amps. How does changing the intensity affect the stopping voltage?

The voltage needed to "stop" the photoelectric current provides an indication of the kinetic energy of the photoelectrons. Recall that the energy of a charged particle in a uniform electric field is defined by E = Vq. In this instance, the equation can be written as Ek = qVstop, where q is the charge of an electron and Vstop is the minimum voltage required to halt the current. Therefore, measuring the voltage required to stop a photoelectric current gives the kinetic energy of the photoelectrons. Graphing the kinetic energy of the photoelectrons (as determined by the stopping voltage) versus the frequency of the incident radiation produces a graphical representation of the photoelectric effect.

SIM 4. Select the electron energy versus light frequency graph () and vary the wavelength (and by extension the frequency) of the incident EMR ().

Sketch the graph of electron energy versus light frequency (as shown below).

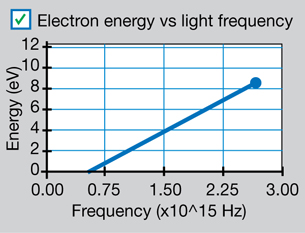
A screenshot of the simulation shows the energy vs. frequency graph.

Your graph should be similar to the following graph, which was presented in Millikan’s 1916 investigation into the photoelectric effect.

A graph of photoelectron kinetic energy vs. incident photon frequency reveals the relationship among all the variables in the photoelectric effect.

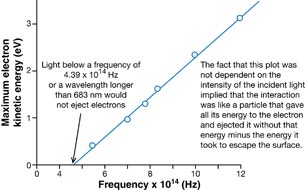
Physics (Pearson Education Canada, 2007) p714, fig 14.12. Reproduced with permission.

This graph is described mathematically by y = mx + b, where y is the kinetic energy of the photoelectrons, x is the frequency of the incident EMR, m is the slope of the line, and b is the y-intercept. Comparing this equation with the conservation of energy gives a mathematical expression for the photoelectric effect. According to the conservation of energy principle, the kinetic energy of the ejected photoelectron is equal to the difference between the energy of the incident photon and the work required to free it from the metal surface (the work function).

This can be stated mathematically (and compared to the graph equation) as follows:

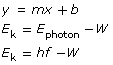
According to this equation, the slope of the line for photoelectron energy versus incident light frequency is equal to Planck’s constant. Therefore, the photoelectric effect provides an experimental way to measure Planck’s constant.

According to the conservation of energy principle, the kinetic energy of the ejected photoelectron is equal to the difference between the energy of the incident photon and the work required to free it from the metal surface (the work function).

Quantity	Symbol	SI Unit
kinetic energy	Ek	J or eV
energy of the incident photon	Ephoton	J or eV
work function of the metal	W	J or eV

The energy of a charged particle in a uniform electric field is defined by

where q is the charge of an electron (1e– or 1.6 × 10–19 C) and Vstop is the minimum voltage required to stop the photoelectric current.

The energy of a photon, according to Planck’s formula is

where c is the speed of light, f is the frequency of the incident radiation and h is Planck’s constant in either joules or electron volts.

h = 6.63 × 10–34 J•s OR 4.14 × 10–15 eV•s

The work function can be defined by the minimum frequency that can cause photoemission, which according to Planck’s formula is , where fo is the threshold frequency (minimum frequency of photon required to cause a photocurrent) and h is Planck’s constant, in terms of joule seconds or electron volts seconds.

Example Problem 1. What is the energy (in J and eV) of a photon of blue light that has a frequency of 6.67 × 1014 Hz?

Given

f = 6.67 × 1014 Hz?

Required

the energy of the photon

Analysis and solution

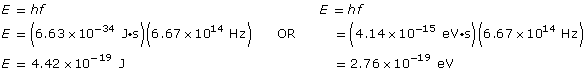
Paraphrase

The energy is 4.42 × 10–19 J or 2.76 eV.

Example Problem 2. Light with a wavelength of 600 nm is directed at a metallic surface that has a work function of 1.60 eV. What is the maximum kinetic energy (in J) of the emitted photoelectrons, their maximum speed, and the voltage needed to stop the photoelectric current?

Given

Required

the kinetic energy of the emitted photoelectrons, their maximum speed, and the voltage needed to stop the photoelectric current

Analysis and Solution

First convert the work function to joules.

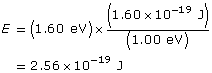
Find the maximum kinetic energy.

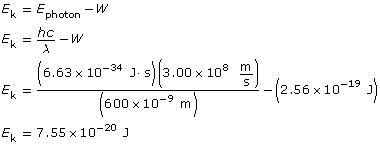
To determine the speed of the photoelectrons, you must use the kinetic energy expressed in joules; eV won’t work due to unit incompatibility!

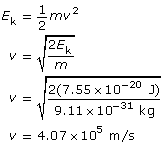
To find the stopping voltage,

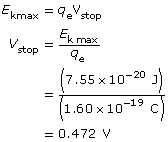
Paraphrase

The kinetic energy of the photoelectrons is 7.55 × 10–20 J; their maximum speed is 4.07 × 105 m/s; and the stopping voltage is 0.472 V.

Example Problem 3. An electron is ejected from a metal with a speed of 4.7 × 106 m/s. The threshold frequency of the metal is 7.8 × 1014 Hz. What is the wavelength of the incident photon?

Given

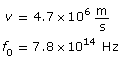
Required

the wavelength of the incident photon

Analysis and Solution

Paraphrase

The wavelength of the photon is 1.9 × 10–8 m or 19 nm.

Self-Check

SC 1. You may check your understanding of the photoelectric effect using this photoelectric effect tutorial.

SC 2. You may check your understanding of the work function using this work function tutorial.

Read

Read “Millikan’s Measurement of Planck’s Constant” on pages 713 to 716 of your physics textbook for more information.

Module 6: Lesson 2 Assignment

Remember to submit your answers to A 1, A 2, A 3, A 4, and A 5 to your teacher as part of your Module 6: Lesson 1 Assignment.

While conducting research into the design of a light sensor, scientists measure the kinetic energy of photoelectrons that have been ejected from an unknown metal surface. The metal is exposed to various frequencies of EMR, and the stopping voltage is measured to obtain the kinetic energy of the photoelectrons. The following data is obtained:

Incident EMR frequency × 1014 Hz	Kinetic energy of photoelectrons (eV)
6.0	0.38
7.0	0.80
8.0	1.20
9.0	1.63
10.0	2.04

A 1. Using this data, plot a kinetic energy versus frequency graph, and use it to answer questions A 2 to A 5. You will find a blank graph in your Module 6: Lesson 1 Assignment.

A 2. According to your graph, what is the threshold frequency of the unknown metal? Label it on your graph.

A 3. Determine the work function of the unknown metal.

A 4. Using “Table 14.1” on page 712 of your textbook, identify the unknown metal.

A 5. Using your graph, determine the experimental value for Planck’s constant (in eV∙s). Label this value on your graph.

Try This

TR 1. Complete “Practice Problems” 1 and 2 on pages 718 and 719 of your physics textbook.

TR 2. If you want more practise, you have the option of trying the Photoelectric Effect Practice Problems.

Module 6: Lesson 2 Assignment

Remember to submit your answers to A 6, A 7, A 8, A 9, and A 10 to your teacher as part of your Module 6: Lesson 1 Assignment.

A 6. What is the energy of a photon that has a wavelength of 460 nm?

A 7. A photoelectric surface has a work function of 2.00 eV. What is the threshold frequency of this surface?

A 8. A photon of frequency 8.2 × 1015 Hz is incident upon a photoelectric apparatus containing a metal whose threshold frequency is 3.6 x 1015 Hz. What is the stopping voltage?

A 9. Electrons are ejected from a photoelectric cell with a maximum kinetic energy of 1.20 eV. If the incident light has a wavelength of 410 nm, what is the work function of the cell?

A 10. Light with a wavelength of 425 nm falls on a photoelectric surface that has a work function of 2.0 eV. What is the maximum speed of any emitted photoelectrons?

Discuss

D 1. You are asked to explain the photoelectric effect in terms of energy to a student who missed the class. In your explanation, start with the energy of the incident EMR photons and finish with the energy of the stopping voltage. Make sure to include the following terms in your answer: threshold frequency, light intensity, photoelectron current, work function, photoelectron kinetic energy, and stopping voltage. Post your answer to the discussion area.

Module 6: Lesson 2 Assignment

Remember to submit your answer to D 2 to your teacher as part of your Module 6: Lesson 1 Assignment.

D 2. Read the answers to D 1 from at least two other students. Revise your answer from D 1 and include any changes you made and how they improved your answer.

Discussion Scoring Guide

Discussion Scoring Guide

Principles involved: Conservation of energy, light energy, electrical energy and voltage
Criteria	Level 1 (Below Standard)	Level 2 (Approaching Standard)	Level 3 (Standard)	Level 4 (Above Standard)
Knowledge
Demonstrates understanding of the situation, physics principles and technology, and their connections.	Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information.	Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation.	Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given.	Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail.
Reflection
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion.	Does not make an effort to participate. Seems indifferent to discussion.	Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion.	Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members.	Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members.
Content and presentation of discussion summary
The information is logically arranged in a clear and concise manner.	The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult.	The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading.	The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences.	The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable.