Module 6

Module 6—Wave-Particle Duality and Quantum Physics

Module Summary

 

In Module 6 you learned about the evidence related to the quantum model and wave-particle duality in relation to blackbody radiation and the photon as a quantum of EMR, the photoelectric effect and the conservation of energy, and the Compton effect and the conservation of momentum and energy.

 

In Lesson 1 you learned about the quantum and how it relates to blackbody radiation. Blackbody radiation refers to a hypothetical object that absorbs all of the electromagnetic radiation that falls on it. The intensity and wavelength (or frequency) of the emitted radiation can be used to construct a blackbody radiation curve. Attempts to explain these curves using classical physics gave nonsensical solutions. Planck was able to explain the blackbody radiation curves by assuming that energy is emitted from hot objects in discrete bundles, or photons, each capable of transferring a minimum quanta of energy associated with its wavelength and frequency according to Planck’s formula, E = hf.

 

You also learned that for physics in general, the idea of the quantum marked the end of classical physics and the beginning of quantum physics by showing that light could be considered a photon, a particle.

 

In Lesson 2 you examined the photoelectric effect experiment and how it supports wave-particle duality. The photoelectric effect showed that light above a threshold frequency is able to cause a potential difference across a metal plate. Einstein explained this effect by using Planck’s quantum hypothesis. Einstein proposed that the energy delivered by a single incident photon is defined by Planck’s formula and that a certain amount of energy, called the work function, is required to free an electron from a metal surface. According to the conservation of energy principle, any extra energy from the photon is contained in the motion of the photoelectron as it leaves the metal surface. These relationships were then verified by Millikan’s experiments using stopping voltage to measure accurately the kinetic energy of the photoelectrons.

 

This gave evidence for Planck’s hypothesis and the particle nature of light. As the wave nature was clearly shown in Unit C, the new theory combined both into the wave-particle duality of light.

 

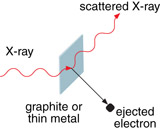
In Lesson 3 you learned about the Compton effect and how it was explained using conservation momentum and energy. When Compton shone an X-ray on a sheet of metal, he observed that the X-ray’s wavelength increased (decreased in energy). He investigated the lost energy and discovered that electrons were ejected from the metal plate. He analyzed the results and saw that energy was conserved but was surprised to see that momentum was also conserved. This gave further supporting evidence for the wave-particle duality.

 

As many physicists were observing the wave-particle duality as it applied to light, de Broglie looked at the wave properties of particles, specifically electrons. He mathematically predicted that high-speed particles would exhibit wave-like properties. His prediction was verified by the electron wave interference, accidentally observed by Davisson and Germer who received the Nobel Prize for the discovery of “matter waves” in 1937. The de Broglie wave equation also explains the quantization of electron energy using resonance and wave interference in a confined space, further supporting quantum theory.

 

All of the concepts presented in this module were designed to help you understand wave-particle duality and quantum theory. In the next module you will see how nuclear reactions in the nuclei of atoms reveal further information about the atom and the fundamental forces that govern the nature of matter.

 

Module Assessment

 

As your module assessment do the following two questions. The first is a holistic question, and the second is a vector question.

 

Question 1

Use the following information to answer this holistic question.

The labels have fallen off two evacuated quartz tubes that have unknown metals at each cathode. One evacuated quartz tube, with Metal X as its cathode, detects visible light leakage from cameras. The other evacuated quartz tube, with Metal Y as its cathode, detects ultraviolet leakage from shielded equipment. A student needs to know which evacuated quartz tube has Metal X and which has Metal Y. The following is one of the evacuated quartz tubes.

 

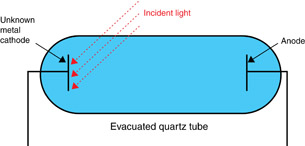
Also available for your experiment are a variable-frequency electromagnetic wave source, a variable voltage source, a voltmeter, and any reference tables needed.

Design an experiment using the photoelectric effect to distinguish between Metal X and Metal Y. Your experimental design must contain the following components:

• statement of the purpose of the experiment
  
• list of the equipment needed
  
• completely labelled diagram of all the equipment necessary
  
• procedure
  
• measurements to be made and recorded and any tables necessary
  
• description of the analysis
• explanation using either the calculation or the derived algebraic equation showing how it will be used to distinguish between Metal X and Metal Y

Holistic Scoring Guide

 

Question 2

Use the following information to answer the following question.

 

A university professor is setting up an example for a class of students. The professor wants to demonstrate Compton scattering of electrons. The professor uses an X-ray machine to project an X-ray with a wavelength of 1.38 × 10–11 m at a thin metal sample. The professor finds that the scattered X-rays have a wavelength of 1.54 × 10–11 m.

 

Determine the

• angle at which the X-rays scatter
• velocity of the ejected electrons (speed and direction), assuming that they start at rest (Ignore any relativistic effects.)

 

Analytic Scoring Guide

 

Physics 30 Learn EveryWare © 2009 Alberta Education