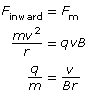Module 7
1. Module 7
1.5. Page 3
Module 7—Investigating the Nature of the Atom
 Watch and Listen
Watch and Listen
Open Determining Charge-to-Mass Ratio (Thomson's Charge/Mass Measurement) to see how Thomson used magnetic and electric fields to determine the charge-to-mass ratio of a particle.
 Try This
Try This
SIM 1. Open the Thomson’s Charge/Mass Measurement simulation.
Adjust the speed slider to match your answer from SC 1. ![]()
Note: The applet reset button changes all of the sliders, so you must adjust them all before repeating the experiment. Notice the difference in the electron’s path if you try different speeds. Predict what the path will be if you change the charge or mass of the particle. Verify your prediction by changing the charge and mass.
This arrangement with a crossed (perpendicular) pair of uniform electric and magnetic fields is called a velocity selector. If charged particles with a variety of velocities enter the fields, only those whose velocity is perpendicular to both fields and whose speed satisfies ![]() will continue in a straight line. The set-up is, therefore, able to select charged particles of a given velocity from all other particles by setting the fields to appropriate values. Velocity selectors have an application in mass spectrometers.
will continue in a straight line. The set-up is, therefore, able to select charged particles of a given velocity from all other particles by setting the fields to appropriate values. Velocity selectors have an application in mass spectrometers.
The arrangement can also be used to measure the speed of charged particles. One must adjust the electric and magnetic fields until there is no deflection and then use the equation to solve for the speed. It is important to note that the value of the speed for which there is no deflection depends on neither the charge nor the mass of the particle. Therefore, you can use a velocity selector to measure the speed of charged particles even if you do not know their charge or their mass.
 Read
Read
Read “Charge-to-mass Ratio of the Electron” on page 755 of your physics textbook.
Part 2: Determining the Charge-to-Mass Ratio of a Cathode Ray Particle
Having determined the speed of the particles as they are coming from the source, you now have to perform a second experiment to determine the charge-to-mass ratio. In the second experiment the particles go through the same apparatus, but with one of the fields turned off. In this circumstance one field will deflect the particles because there is no other force from the other field to balance it.
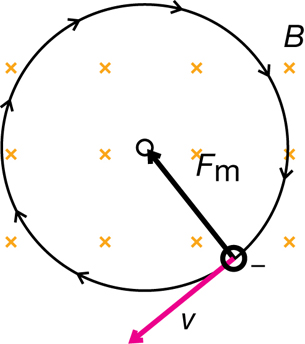
Recall that a magnetic force will produce a perpendicular force on a moving charge as determined by the hand rule. The uniform perpendicular force will cause the charged particle to move along a circular path of constant radius. Therefore,
Finward = Fm
Given the definitions of the inward, centripetal force and the magnetic force, it is possible to derive an equation for the charge-to-mass ratio of the particle exhibiting circular motion in the magnetic field alone.
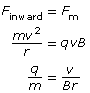
In a Thomson-style experiment, the velocity is first determined using both a known magnetic and electric field. Then, by turning off the electric field and measuring the radius of the circular path made by the charged particles, you would be able to determine the charge-to-mass ratio of the particles.
Thomson determined that the charge-to-mass ratio of the particles in a cathode ray was 1.76 × 1011 C/kg. This value was unique to all cathode rays regardless of the metal electrodes used to produce them. Thomson had discovered the electron, but, more importantly, he had determined that the charge-to-mass ratio for an electron was thousands of times larger than that of a hydrogen ion, which meant that the electron was a “subatomic” particle. He proposed a radical idea at the time—the atom was divisible into smaller particles. And since no positive subatomic particles had been discovered at the time, he suggested that the atom consisted of electrons embedded in a blob of massless positive charge, what is now known as the raisin-bun model of the atom. You will learn more about this model later on in the lesson.
 Read
Read
Read “Determining Charge-to-mass Ratios” on pages 757 to 758 of your physics textbook.
 Self-Check
Self-Check
SC 3. Using the charge and mass values on your physics data sheet, what is the charge-to-mass ratio of
- the proton
- the alpha particle
- the neutron
SC 4. How many times larger is the charge-to-mass ratio of the electron than the proton?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3.
- Proton
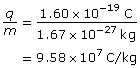
The charge-to-mass ratio of the proton is 9.58×107 C/kg.
- Alpha particle
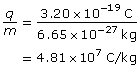
The charge-to-mass ratio of the alpha particle is 4.81×107 C/kg.
- Neutron
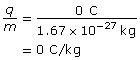
The neutron is neutral, so it has no charge; as a result, the charge-to-mass ratio is zero.
SC 4.
Given
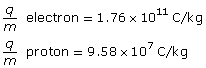
Required
the number of times larger the electron’s charge-to-mass ratio is than the proton’s charge-to-mass ratio
Analysis and Solution
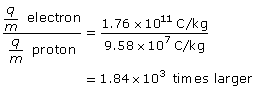
Paraphrase
The charge-to-mass ratio of the electron is 1.84×103 larger.
In order to obtain the charge and mass values on the physics data sheet, experimental data was analyzed. Here are some examples of how that can be done.
Example Problem 1. A charged particle is travelling horizontally at 3.60 × 106 m/s through a vertical magnetic field of 0.710 T. If the radius of the curvature of the particle’s path is 0.950 m, what is the charge-to-mass ratio of the particle?
Given
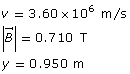
Required
the charge-to-mass ratio of the given particle
Analysis and Solution
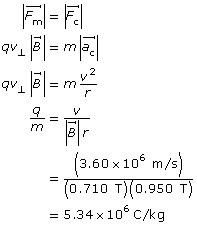
Paraphrase
The charge-to-mass ratio of the particle is 5.34×106 C/kg.
Example Problem 2. What is the speed of an electron that passes through an electric field of 6.30 × 103 N/C and a magnetic field of 7.11 × 10-3 T undeflected? The two fields are perpendicular to each other and to the path of the electron. What is the kinetic energy of the electron?
Given
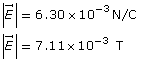
Required
the kinetic energy of the electron
Analysis and Solution
Find the velocity by balancing the force magnetic with the force electric.
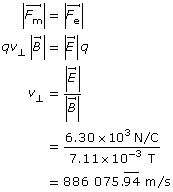
Find the kinetic energy.
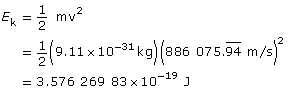
Paraphrase
The kinetic energy of the electron is 3.58×10–19 J.
 Try This
Try This
TR 1. An alpha particle travels through a magnetic field of 0.422 T perpendicular to the field. If the radius of arc of the deflected particle is 1.50 × 10–3 m, what was the speed of the alpha particle? (3.05×104 m/s)
TR 2. A proton travels through a magnetic field at a speed of 5.40 × 105 m/s, perpendicular to the field. If the radius of curvature is 7.20 mm, what is the magnetic field strength? (0.783 T)
TR 3. Alpha particles travel undeflected through magnetic and electric fields that are perpendicular to each other. If the speed of the alpha particles was 7.80 × 105 m/s and the magnetic field strength was 0.220 T, what was the electric field strength? (1.72 × 105 N/C)
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit your answers to A 2, A 3, A 4, and A 5 to your teacher as part of your Module 7: Lesson 1 Assignment.
A 2. What is the charge-to-mass ratio of a particle travelling 3.60 × 105 m/s that is deflected in an arc of radius 7.40 cm as it travels through a magnetic field of 0.610 T?
A 3. Some positively charged particles are found to pass undeflected through perpendicular magnetic and electric fields. The magnetic field strength is 0.650 T, and the electric field strength is 2.10 × 105 N/C. What is the speed of the particles?
A 4. Alpha particles travel through a magnetic field of 0.360 T and are deflected in an arc of 0.0820 m. Assuming the alpha particles are perpendicular to the field, what is the energy of an individual alpha particle?
A 5. Using the charge of an electron (determined by Millikan in another experiment to be 1.60 × 10–19 C and the charge-to-mass ratio of the electron (determined by Thomson to be 1.76 × 1011 C/kg), calculate the mass of an electron.
 Watch and Listen
Watch and Listen
Thomson’s experiment was about more than just finding the electron; it was also about understanding that matter could be divided into smaller parts. Watch the video “The Millikan Experiment” to see the glow emitted by a cathode ray tube, Thomson’s apparatus, and hear about his groundbreaking work, which effectively demonstrated that the atom was made of divisible parts.
 Self-Check
Self-Check
SC 5. Explain how Thomson calculated the unique charge-to-mass ratio for an electron by completing the following statements and equations.
Step 1: Determine the velocity of the electrons by measuring the_______________ and _______________ fields and using this equation:
_________________
Step 2: Turn off the _____________ field, leaving only the __________ field, which acts perpendicularly to the velocity of the charged particle. In this orientation the magnetic force causes the charged particle to exhibit ________ motion, giving the following expression for the charge-to-mass ratio:
_________________
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 2.
Step 1: Determine the velocity of the electrons by measuring the electric and magnetic fields and using this equation:
![]()
Step 2: Turn off the electric field, leaving only the magnetic field, which acts perpendicularly to the velocity of the charged particle. In this orientation the magnetic force causes the charged particle to exhibit uniform circular motion, giving the following expression for the charge-to-mass ratio: