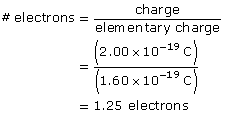Module 7
1. Module 7
1.9. Page 2
Module 7—Investigating the Nature of the Atom
 Explore
Explore
The Millikan Experiment
Shortly after Thomson confirmed the existence of the electron with a charge-to-mass ratio, physicist Robert Millikan designed and performed an experiment to determine the charge on an electron. His well-known oil drop experiment involved spraying tiny oil droplets into a vertical chamber with two metal plates on either end. The oil droplets became charged in the spraying process and when they entered the chamber, they began to fall under the influence of gravity. Millikan could then stop the free-falling droplets and reverse their direction of motion by applying a voltage across the two metal plates. Using a microscope and a timer, he measured the velocity of a single oil droplet in the electric field in order to determine the electrical force acting on it. This allowed him to determine the charge on the oil droplet, since ![]() .
.
It is important to recognize that the charge on the oil droplet was likely due to the presence of many, many extra electrons. Therefore, the charge of an oil droplet will be an integer multiple of the charge on a single electron. Do not confuse the charge of the oil droplet with the elementary charge of a single electron.
How could Millikan determine the charge of a single electron using the charge on multiple oil droplets? By measuring the charge of many droplets and comparing them, he reasoned that the smallest difference in charge among all the droplets would be due to the presence of one extra electron. That small difference in charge would then be equal to the charge of a single electron or the elementary charge. Using the charge on numerous oil droplets and through careful analysis, Millikan discovered that the charges of the oil droplets were always integer multiples of 1.602 × 10–19 C.
elementary unit of charge: the charge of an electron or a proton, 1.60 × 10–19 C
 Watch and Listen
Watch and Listen
Watch the video “The Millikan Experiment: Part 2” to see Millikan's experimental design and apparatus.
How did Millikan’s Apparatus Work?
Open the “Millikan Experiment Simulation” to explore the experimental design.
The apparatus consists of a chamber (as shown below). Looking through the eyepiece, you would see something similar to that shown in the “Reticle View” mode. To switch to the reticle view, click the view button (

Open “Determining the Elementary Charge: Millikan's Oil Drop Experiment” to see how Millikan's oil drop experiment is used to determine the elementary charge.
 Module 7: Lesson 2 Assignment
Module 7: Lesson 2 Assignment
Remember to submit your answers to LAB 1 to your teacher as part of your Module 7: Lesson 2 Assignment.
LAB 1. Use the following procedures to re-enact Millikan’s experiment.
- On the simulation, select the reticle view (
 ) and make sure that the electric field is off (
) and make sure that the electric field is off ( ).
).
- Inject oil droplets into the apparatus by clicking the inject button (
 ) a few times. You should see the droplets moving down.
) a few times. You should see the droplets moving down.
- Toggle the field on and off a couple of times (
 or shortcut key V). When the field is on, you should see some of the droplets move up.
or shortcut key V). When the field is on, you should see some of the droplets move up.
- Look for a droplet that moves both up and down slowly. Select this droplet by clicking on it with your mouse, and verify that it changes colour.
- When your selected droplet is well above the top line of the reticle, turn the field off. As the droplet is falling,
- start the timer (
 or shortcut key M) when it passes the top line of the reticle
or shortcut key M) when it passes the top line of the reticle
- stop the timer (
 or shortcut key M) when it passes the bottom line of the reticle (this is the fall time)
or shortcut key M) when it passes the bottom line of the reticle (this is the fall time)
- start the timer (
- After the droplet has passed the bottom line of the reticle, switch the field on. As the droplet is rising,
- start the timer (
 or shortcut key M) when it passes the bottom line of the reticle
or shortcut key M) when it passes the bottom line of the reticle
- stop the timer (
 or shortcut key M) when it passes the top line of the reticle (this is the rise time)
or shortcut key M) when it passes the top line of the reticle (this is the rise time)
- start the timer (
- Repeat steps 5 and 6 five times for your selected droplet.
- Click the data button (
 ) and view the “Collected Data.” Millikan used the rise and fall times, the mass of the droplet (determined by volume and density), and forces related to air resistance to determine its charge. Note that you will see information related to these values when you click
) and view the “Collected Data.” Millikan used the rise and fall times, the mass of the droplet (determined by volume and density), and forces related to air resistance to determine its charge. Note that you will see information related to these values when you click  and select the “Data Analysis” tab.
and select the “Data Analysis” tab.
LAB 1. Record the average rise velocity: _______________________ average fall velocity: _______________________ charge of your oil droplet: _______________________
Although time-consuming, Millikan’s experiment was instrumental in establishing not only the value of the elementary charge, but also the quantized nature of electric charge. This follows Planck’s earlier discovery that energy is also quantized.
Building on Thomson’s work with the charge-to-mass ratio of an electron, it was then possible to determine the mass of an electron as 9.11 × 10–31 kg.
From J. J. Thomson:
![]()
From R. A. Millikan:
![]()
Combined:
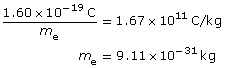
Due to rounding and significant digits, the value is extremely close to the accepted mass of the electron 9.11×10–31 kg.
By accelerating hydrogen ions (protons) through a potential difference and determining their charge-to-mass ratio, it was found that their mass was 1.67 × 10–27 kg. Together, Thomson and Millikan had essentially weighed and measured the charge of some of the smallest fundamental particles that make up matter. They also confirmed the idea that the atom was not the smallest form of matter and that it had divisible parts.
Analysis of Millikan’s Experiment
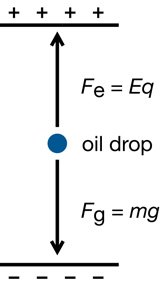
Millikan’s original analysis can be simplified by assuming that the droplets can become suspended between the plates (eliminating any drag forces). That meant that the droplets experienced an electric force upward, exactly equal to the gravitational force pulling them down.
If a droplet were suspended, then the electrical force pulling it up would exactly balance the gravitational force pulling it down. Therefore,
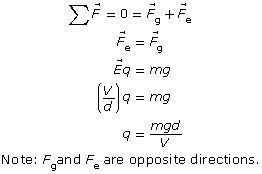
 Read
Read
Read “Millikan’s Oil-drop Experiment” on pages 761 to 764 of the textbook.
Example Problem 1. An oil droplet with a mass of 9.80 × 10–16 kg is suspended between two horizontal charged plates. If the electric field strength between the plates is 2.0 × 104 V/m, what is the charge on the oil droplets?
Given
![]()
Required
the charge on the oil drop
Analysis and Solution
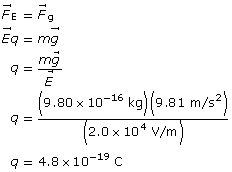
Paraphrase
The charge on the drop is 4.8×10–19 C.
Example Problem 2. An oil droplet with a weight of 4.80 × 10–14 N is suspended between two horizontal charged plates that are 5.00 cm apart. If the potential difference between the plates is 3.0 × 103 V, how many excess electrons does the oil droplet carry?
Given
![]()
![]()
![]()
Required
the number of excess electrons the oil drop carries
Analysis and Solution
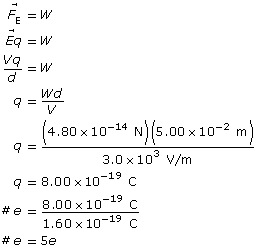
Paraphrase
The oil drop has five excess electrons.
 Self-Check
Self-Check
SC 1. An oil droplet weighs 3.84 × 10–15 N. If it is at rest between two horizontal plates with an electric field strength of 1.20 × 104 N/C, what is the charge on the oil droplet?
SC 2. An oil droplet with a mass of 4.80 × 10–16 kg is suspended between two horizontal charged plates that are 6.00 cm apart. If the potential difference between the plates is 588 V, how many excess electrons are on the droplet?
SC 3. Is it possible to have a particle with a charge of 2.00 × 10–19 C? Explain why or why not.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Given
![]()
Required
the charge on the particle
Analysis and Solution
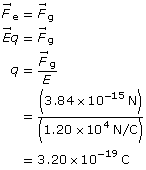
Paraphrase
The charge on the particle is 3.20 × 10–19 C.
SC 2.
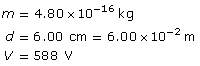
Required
the quantity of excess electrons on the particle
Analysis and Solution
Start with the two equal forces.
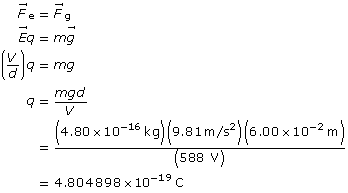
Determine the number of electrons required to obtain the charge.
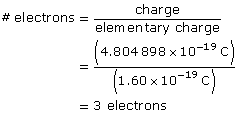
Paraphrase
The particle has three excess electrons.
SC. 3
No, it is not possible to have a charge of 2.00 × 10–19 C because it is not possible to have a quarter of an electron. It is only possible to have whole number multiples of 1.60 × 10–19 C; the charge must be 1.60 × 10–19 or 3.20 × 10–19 or 4.80 × 10–19 C, etc.