Module 7
1. Module 7
1.15. Page 4
Module 7—Investigating the Nature of the Atom
Reflect and Connect
The Bohr model of the atom, in conjunction with spectroscopy, can be used to identify unknown gases based on either their absorption or emission line spectrums. The missing parts of the sun’s spectrum can be explained using the absorption spectrum of hydrogen and helium, indicating their presence on the surface of the sun.
Using a similar technique, it is possible to identify the chemical composition of other stars and galaxies by examining the wavelengths of light that come from them.
RC 1. Open the Star Spectra Simulation and see if you can identify the presence of known elements using the line spectrum from astronomical objects such as stars and galaxies.
Going Beyond—The Quantum Mechanical Model of the Hydrogen Atom
With the development of quantum mechanics throughout the 20th century, a quantum mechanical model of the atom has been devised. Bohr’s model of the hydrogen atom was a semi-classical model—it took ideas from classical physics and extended them to quantum physics. A quantum mechanical model of the hydrogen atom does not rely on classical physics; rather, it is built upon ideas of wave functions and probabilities.
In the quantum model of the atom, electrons do not exist in specific orbits around a nucleus. Rather, the quantum model computes probabilities for the location of an electron around a nucleus. Remember that Bohr’s model stated that an electron can only exist in specific orbits, with a specific energy and radius. The quantum model denies these absolute ideas. An electron can exist anywhere around a nucleus—the probability distribution represents the most likely location of the electron.
The Hydrogen Atom Simulation can be used to compare the quantum model of the hydrogen atom to Bohr’s model of the hydrogen atom. On the simulation, the allowed Bohr radii are drawn as circles. Remember that the scintillations (flashes of light) represent probabilities—the brighter the flash, the greater the probability.
Self-Check
SC 5. Play the Hydrogen Atom Simulation and select the probability cloud mode (
). Make sure that the electron is in its ground state (n = 1). Vary the scintillation rate using the slider.
- The diagram below shows the first three allowed Bohr radii for hydrogen. On a diagram like the one shown, sketch the probability density for an electron in the ground state (n = 1), according to the quantum mechanical model of hydrogen. Indicate the region(s) of highest probability on your diagram.
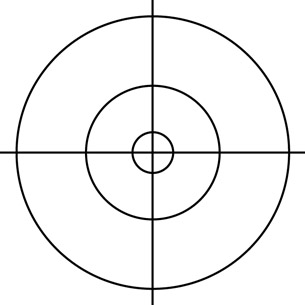
- How does the quantum mechanical model for the ground state of hydrogen compare to the Bohr model for the ground state?
SC 6. Reset the simulation so that the electron is in the ground state (n = 1). Do a transition to the second energy level. Again, vary the scintillation rate and toggle between modes.
- Sketch the probability density for an electron in the second energy level. Indicate the region(s) of highest probability on your diagram.
- How does the quantum mechanical model for an electron in the second energy level of hydrogen compare to the Bohr model for the ground state?
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 4.
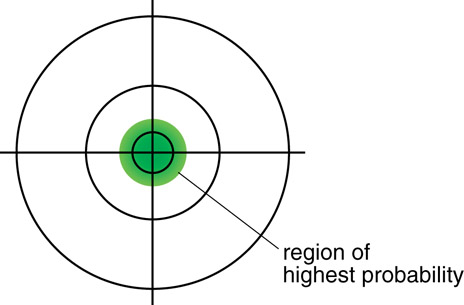
- The quantum mechanical model is illustrated using a wide probability density cloud, but at a distance farther from the nucleus than the thin circular line of the Bohr model for the ground state.
SC 6.
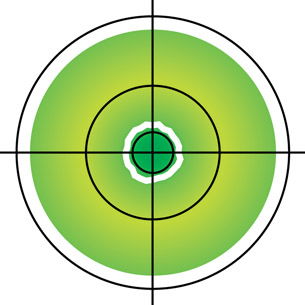
- The quantum mechanical model is illustrated using a wide probability density cloud, whereas the Bohr model is illustrated by thin, circular lines.
Module 7: Lesson 3 Assignment
Remember to submit the Module 7: Lesson 3 Assignment to your teacher.