Lesson 3: Basic Measurement Systems and Conversions
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 3: Basic Measurement Systems and Conversions |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:25 AM |
Focus

Many young people dream of the time when they will plan and build their own house and make it their own place. Moving from planning blueprints to the construction stage is one time when measurement conversion becomes important. Measurements are critical to a successful construction process.
Using referents, or relating measures to common objects, allows you to estimate measurements quickly. Would it be appropriate to construct a house using referents only?
In the last lesson you focused on how to take the measurements of various shapes. In this lesson you will learn how to perform measurement conversions within each the SI and the imperial system. You will also learn how to perform measurement conversions between the SI and the imperial system.
You will begin the lesson by estimating using body parts as referents. Then you will use ratios and proportion to solve problems. You will answer questions like the following:
-
How many inches are there in a foot?
-
How many millimetres are there in 10 cm?
-
How do you convert kilometres to miles?
Outcomes
At the end of this lesson, you will be able to
-
explain how proportional reasoning can be used to convert a measurement within or between the SI and the imperial system
-
solve a problem that involves the conversion of units
-
verify, using unit analysis, a conversion within or between the SI and the imperial system and explain the conversion
-
justify, using mental mathematics, the reasonableness of a solution to a conversion problem
Lesson Questions
-
How do the strategies for converting units in the SI compare with those used in the imperial system?
-
When can proportions be used to solve problems?
![]() Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Launch
Are you Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. What is the rule for multiplying fractions?
2. Multiply each pair of fractions. Simplify, where possible.
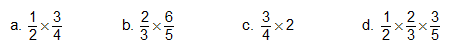
3. What is meant by the expression equivalent fractions?
4. Find the missing term to complete the equivalent fraction.
![]()
5. Fill in the blanks:
a. 1 m = __________ cm
b. 1 cm = _________mm
c. 1 km = _________m
d. 1 ft = _________ in
e. 1 yd =_________ ft
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
![]() Refresher
Refresher
Review how to multiply fractions by completing the multimedia piece titled “Multiplying Fractions.”
Try the interactive applet “Equivalent Fractions” to brush up on equivalent fractions.
To navigate to the correct lesson, do the following:
-
Choose “Fractions and Equivalent Fractions (Home)” in the left-hand column.
-
Then choose “Topics” in the upper left-hand corner.
-
Select “4. Equivalent Fractions.”
-----------------------------------------------------------------

© Nikolay Okhitin/shutterstock
Blueprints are the basic planning documents for building houses. On a blueprint, all of the dimensions of a home are drawn to scale. This means that a specific length in the blueprint equals a specific distance in real life. The ratio is the same for all of the lengths. If you know what the ratio or scale is for a blueprint, then you can convert the measures on the diagram into actual measures.
You can convert measurements within the SI or the imperial system. You can even convert measurements between the two systems. To do so, you need to understand the concepts of ratio and proportion.
![]() Watch and Listen
Watch and Listen
Go to “Exploring Rate, Ratio and Proportion.”
(Make sure you maximize the screen by clicking on the button in the top-right corner of the video.) The website features both a video and an interactive piece. First, view the video. On the left-hand side of the page, select “Exploring Rate, Ratio and Proportion (Video Interactive).” Then try the interactive component to refresh your understanding of ratio and proportion. Click on the “Interactive” button on the right-hand side of the website.
Materials
-
results from Math Lab: Body Referents in Lesson 1
-
calculator
Discover and Explore
Discover
When you convert measurements, you need to know how units of measurement relate to each other. For example, you should know from your previous math studies that 1 cm = 10 mm or 1 ft = 12 in (see questions 5.b. and 5.d. in Are You Ready?). But do you know how many millimetres there are in a kilometre or how many kilometres there are in a mile?
Print (or copy out by hand) the following document SI and Imperial Conversions Sheet. Use your formula sheet or google to find the correct relationships between the SI units and the imperial units stated on the sheet. Complete the sheet by writing the correct numbers in the blanks.
Use the following link to check your work.
Explore

© iofoto/shutterstock
Glossary Terms
Find the “Glossary Terms” document that you printed earlier. Add the following words to the document:
-
unit analysis
-
unit conversion
You may also choose to add other terms to help you understand the math you are studying
You learned in a previous lesson that both the SI and the imperial systems are used in the trades. In order for two tradespeople who use different measurement systems to understand each other, it may be necessary to use measurement conversions.
You can begin your study of measurement systems by examining conversions within the SI.
Use the multimedia piece titled “International System of Units” to explore unit conversions within the SI.

Pay close attention to the following:
-
basic units
-
prefixes
-
conversions
---------------------------------------------------------------------------
Here are some examples of problems you might encounter when it comes to unit conversions.
Example: Converting Between SI Units
Problem
Convert 450 cm to millimetres and kilometres.
Solution
One way that you can solve a conversion problem is to set up a proportion, and then use cross-multiplication to find the answer.
Since 1 cm = 10 mm,
![]()
The variable x will be in units of centimetres.
Then,

There are 4500 mm in 450 cm.
Another way that you can solve a conversion problem is to use the technique of unit analysis. Unit analysis helps you to keep track of the measurement units to ensure that your result will be expressed in the correct units.
Recall that 1 m = 100 cm and 1 km = 1000 m. If you want the final result to be expressed km, you can show your work in the following way:

There is 0.0045 km in 450 cm.
Example: Converting Between Imperial Units
Problem
On a particular Canadian Football League team, the average height of the players is 6 ft 3 in.
First, determine how tall the average football player is in inches only on this team.
Second, figure out, on average, how many of these football players, lined up head to toe, it would take to stretch across a regulation football field with length 110 yards.
Solution
You already have part of the height in inches, so you just need to convert 6 ft into inches, before adding the extra 3 in.
Since 1 ft = 12 in,
![]()
The variable x will be in inches.
Then,

There are 72 inches in 6 ft.
Therefore, the average height is 72 + 3 = 75 in.
Next, you can use the unit analysis method to convert 110 yd to inches. Then you can determine how many times 75 in goes into the result.
Recall that 1 ft = 12 in and 3 ft = 1 yd.
So,

The football field is 3960 in.
Now, 3960 in ÷ 75 in = 52.8.
Therefore, it would take about 53 football players, lying head-to-toe, to line the length of a CFL football field.
Explore 2
![]() Try This
Try This
Please complete the following exercises in your course folder ( binder).
TT 1.(Try This 1) Complete “Exercises” questions 7, 8, 11, and 18 on pages 11 and 12 of your textbook.
Use the link below to check your work.
The next step is to learn how to convert measurements between the SI and the imperial system. In the Math Lab: Body Referents in Lesson 1, you established referents for both measurement systems. You can use these referents to make sure each of your calculations is reasonable.
To do so, you would estimate the answer using an appropriate referent; then compare your estimate with your calculation. If the numbers are close, then your calculation is reasonable. If the numbers are different, stop to think about why the numbers are different and where you might have gone wrong in your calculations. Keep this in mind as you read the next section. You will have an opportunity to use referents to estimate in a subsequent Self-Check section.
![]() Read
Read
How do you convert between SI and imperial units? The strategies to do this are the same as those used in the previous conversions. The first thing you have to do is find out the relationship between the units. Once you know this, you can either set up a ratio or prepare to convert using unit analysis.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Converting from Metres to Feet” on page 18 to see how a measurement in metres is converted to an equivalent measure in feet.
Read “Example 2: Converting between Miles and Kilometres” on page 19 to see two methods for solving a problem involving a conversion between miles and kilometres.
When you are done, you can test yourself in the Self-Check section.
![]() Self-Check
Self-Check
For each of the following, choose the correct answer.
SC 1. A measure of 2 cm is (larger than, smaller than) an inch.
SC 2. A measure of a mile is (larger than, smaller than) a kilometre.
SC 3. A measure of a yard is (larger than, smaller than) a metre.
SC 4. A measure of 25 cm is (larger than, smaller than) a foot.
SC 5. Convert 90 in to yards, demonstrating unit analysis. For this question, please show all your steps to the solution.
![]() Try This
Try This
Please complete the following exercises in your course folder ( binder).
TT 1.(Try This 1) Complete “Exercises” questions 9, 11, 14, and 16 on pages 22 and 23 of your textbook.
Use the link below to check your work.
![]() Share
Share
You now have learned several ways of converting measurements from one unit to another. You can convert measurements by setting up a proportion and using cross-multiplication. Alternatively, you could use unit analysis. You also have an idea of how metric units compare to imperial units.
Can you describe why working with proportions is a good strategy for doing unit conversions? Have you developed other strategies of your own? Discuss these questions with another student or appropriate partner (if possible). Save your answers in your course folder ( binder).
Connect
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or using the Quizzes link under the Activties block. Also ensure your work in your binder (course folder) is complete.
![]() Going Beyond
Going Beyond

© Catalin D/shutterstock
This is an illustration that depicts Leonardo da Vinci’s Vitruvian Man. It is famous for showing a man in proper mathematical proportions.
We use measurements and proportion in many aspects of our lives. Artists use proportion to know how to draw the human form:
-
The head and neck are about one-sixth the length of the body.
-
The legs are one-half the length of the body.
-
The upper arm is about equal to the length of the head.
-
The lower arm to the wrist is about equal to the length of the foot.
-------------------------------------------------------------------------------------------------

© Rafa Irusta/1238019/Fotolia
Measurement conversions are an important part of many occupations, and errors can have disastrous results. Imagine what could happen if you made an error while calculating the amount of fuel that is needed for an airplane. In 1983, this very thing happened in Canada!
Perform an Internet search using the term “Gimli Glider.” In your research, try to find out where the improper use of measurement conversions led to the incident.
Can you find any other similar situations? If you find any other examples, save them in your course folder in case your teacher would like to compile the various examples.
Summary
-
How do the strategies for converting units in the SI compare with those used in the imperial system?
-
When can proportions be used to solve problems?
In this lesson you learned how proportional reasoning can be used to convert a measurement within or between the SI and the imperial system.
The SI is based on powers of 10. As a result, conversions in the SI system involve multiplication or division by 10, 100, 1000, and so on.
The imperial system, on the other hand, is not based on powers of any specific value. When using the imperial system, it is more advantageous to set up a proportion. Proportions are best suited to solving problems when an equivalent relationship can be established. Once the proportion is established, you can convert first by cross-multiplying and then by dividing.
You also learned to verify using unit analysis. Unit analysis helps you to convert measurements by cancelling unwanted units. In addition, you solved problems that involve the conversion of units and justified, using mental mathematics, the reasonableness of the solution.
Now continue on to Lesson 4 of this module.

