Lesson 4: Surface Area of 3-D Objects
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Surface Area of 3-D Objects |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:25 AM |
Focus

Now that you are familiar with estimating and converting between SI (metric) units and imperial units, you will expand your knowledge to include 3-D objects that include curved surfaces. These objects include cylinders, spheres, cones, prisms, and pyramids. You will use the skills gained in Lesson 2 where you explored measuring curved surfaces.
Our surroundings are full of various 3-D objects, many of which can be broken into smaller, basic objects whose surface area and volume can be calculated. You will investigate surface area in this lesson, and by the end of this lesson you will be able to apply and use the surface area calculations needed in your project.
Outcomes
At the end of this lesson, you will be able to solve, using SI and imperial units, problems that involve the surface area of objects, including:
- right cones
- right cylinders
- prisms
- pyramids
- spheres
Lesson Questions
By the end of this lesson you should feel comfortable solving the following questions:
- How is the concept of surface area applied to understanding the design of structures?
- How do you determine the surface area of a 3-D object?
![]() Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Launch
Are you Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
You will use this illustration to answer questions 1 and 2.
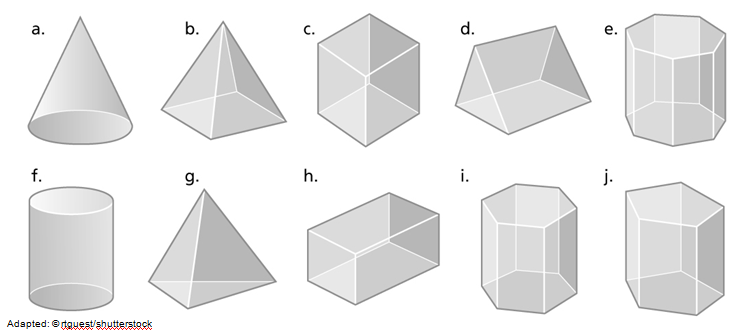
2. Look at the 3-D objects in the illustration. Identify them either as prisms or pyramids.
3. What does area mean?
4. Show the formula for the area of a
a. rectangle
b. triangle
c. circle
5. Determine, to the nearest tenth of a cm2, the area of the following shapes:

Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
![]() Refresher
Refresher
How did you do? Did you remember the difference between a prism and a pyramid? Did you remember how to find the area of basic shapes? Great work, if you remembered! If you did not remember, please carefully read this Refresher section.
Let’s take a look at what area means and how to find areas of basic shapes. This information will not only be helpful as you prepare to find the surface area of objects in this lesson but also when you explore the volume of those objects in the next lesson.
Area Definition
The Mathematics Glossary defines the term area. Go to “Area” to learn more. It contains an interactive Java applet and Flash animations to illustrate the definition. (Username is LA53, password is 4487 if needed.)
-----------------------------------------------------------------------------------------
Finding Area with Unit Squares
The mathematics lesson “Finding Area with Unit Squares” explores the measurement of square units. The lesson presents the formulas for the area of a rectangle, parallelogram, and triangle, and it includes math problems that involve the practical application of these formulas.(Username is LA53, password is 4487 if needed.)
-----------------------------------------------------------------------------------------
Estimating Area Using a Grid
The mathematics lesson “Estimating Area Using a Grid” uses inscribed polygons, circumscribed polygons, and the concept of limits to explain how the area of a circle can be measured. The lesson includes a game and a math problem that demonstrate the practical application of the formula for the area of a circle.
Materials
- paper
- prism net and pyramid net
- soup can with label
- scissors
- scotch tape
- a rectangular prism, such as a wooden block, a shoe box, or a cereal box
You will also require these materials to complete Math Lab: The Surface Area of an Orange:
- orange
- string
- ruler
Discover

© Max Krasnov/shutterstock
![]() Math Lab: The Surface Area of an Orange ** OPTIONAL TO COMPLETE**
Math Lab: The Surface Area of an Orange ** OPTIONAL TO COMPLETE**
Go to Math Lab: The Surface Area of an Orange, print it (or copy by hand) and complete it. You are asked to post to the discussion board L4: Discussion Board Posting - Orange Math Lab.
Keep this in your course folder (binder) as you will need to refer to it later in the lesson.
In order to complete the Math Lab, you will need to go to 1 cm × 1 cm Grid Paper and print a copy.
Explore
In this lesson the suggested glossary terms to add are the following:
- 3-D object
- apex
- lateral area
- net
- prism
- pyramid
- regular polygon
- right cone
- right cylinder
- sector
- sphere
- surface area
-----------------------------------------------------------
Imagine taking a 3-D object and submerging it in a tub of water. The area of the object that is in contact with the water is called the surface area. You can also think of surface area as the measure of how much exposed area that a solid object has.
How would you determine the surface area of an object?
One way to do determine the surface area of the object is to peel off the outer layer of the object and then calculate the area of the peel. The peel is called the net. In Math Lab: The Surface Area of an Orange, you obtained a net of the orange (i.e., the orange peel sections) and added the areas of each part of the net (i.e., each peel section) to obtain the surface area of the orange.
As you move through this lesson, you will examine the nets of other 3-D objects. By adding together the sections of a net, you can determine the surface area of those objects.
![]() Watch and Listen
Watch and Listen
Use "Surface Area of Prisms" to find out how to use the net of a rectangular prism to determine its surface area.
--------------------------------------------------------------------------
then watch “Surface Area of Prisms 2 ” to see another example of the net of a rectangular prism used to determine its surface area.
-----------------------------------------------------------------------
![]() Try This: Prisms, Pyramids, and Cylinders
Try This: Prisms, Pyramids, and Cylinders
Work with a partner (if possible) to examine the nets of prisms, pyramids, and cylinders. Use the following document titled Surface Area and Volume Investigation (or copy by hand) to summarize the information you will collect during this investigation. You may want to use the materials outlined in the Launch section as part of the investigation.
- paper
- prism net and pyramid net
- soup can with label
- scissors
- scotch tape
- a rectangular prism, such as a wooden block, a shoe box, or a cereal box
- toblerone box if possible
For each 3-D object, create a net that can be easily folded into the 3-D object. To get started, you can use the following descriptions. However, you are not limited by the descriptions. You are free to use other ways of creating a net for the object.
Remember to add the information you discover to your “Surface Area and Volume Investigation” document. Then save a copy of your completed handout in your course folder.
Use the cereal box to create the net of a rectangular prism.
- Carefully unfold the cereal box and flatten it.
- Cut off any flaps that are not part of the surface area. (Some flaps will remain because they are a part of the exterior of the box.)
Use an empty Toblerone box to create the net of a triangular prism.
- Carefully unfold the box and flatten it.
- Cut off any flaps that are not part of the surface area.
To create a net of a square pyramid, go to Square Pyramid Net and print a copy.
- Cut out the net.
- Fold along the lines so it forms a three-dimensional pyramid.
Use the soup can with a label to create a net of a cylinder. For an idea of how you can do this, follow this procedure.
- Trace each circular end onto a sheet of paper.
- Cut out each of the ends.
- Remove the label from the soup can.
- Tape the circular ends to the label so that the net can be rolled into a 3-D cylinder.
![]() Try This
Try This
TT 1. For each net, describe how many sections there are in the net.
TT 2. For each net, describe what dimensions will be needed to determine the areas of each section.
TT 3. For each net, describe what the formula for the surface area could look like. Try to match the formula below to each shape:
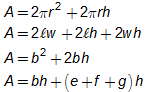
Use the link below to check your answers to Try This 1 - 3.
Here is a great video that shows you how to find Surface Area of a Right Rectangular prism
![]() Read
Read
Read the textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Determining the Surface Area of a Right Rectangular Triangle” on page 29 to see how a formula can be used to determine the surface area of a rectangular pyramid. Try to see what needs to be determined before the formula can be applied.
![]() Self-Check
Self-Check
You have seen in the examples how a formula is applied in finding the surface area of a pyramid. Now use the formulas that you created to find the solutions to the following problems.
SC 1. Determine the surface area of the following pyramid, to the nearest in2.

SC 2. Determine the surface area of the cylinder to the nearest cm2.

Note the answer to SC2 is 150.8 cm2. Typo in the answer.
SC 3. Determine the surface area of the following prism, rounded to the nearest cm2.

SC 4. Consider the net shown. What does this net represent?

- A cube with a side 10 cm.
- A box with a length and width 10 cm and a height 5 cm.
- A box with a length and width 5 cm and a height 10 cm
- This net does not represent a box.
![]() Did You Know?
Did You Know?

While the pyramids of the ancient Egyptians are likely recognized by most people with their square bases and four smooth triangular sides, other ancient civilizations also constructed pyramids with slightly different designs. The Aztec and Mayan pyramids were built with tiered steps and a flat top instead of smooth sides and a peak.
Explore 2
![]() Try This
Try This
Review the results you obtained for your Math Lab data and analysis. In your analysis of the results, you evaluated the ratio . You also looked at what other students obtained for this ratio. Did you find that the ratio was close to 3.14? In fact, under ideal circumstances, this ratio would be π.
TT 4. What might be some reasons why someone doing the Math Lab did not get a number that was close to π?
Use the link below to check your answers to Try This 4.
Possible TT4 ( Try This 4) Solutions
Now, see what happens if you take the ratio and rearrange it.

You can take the formula further by substituting d = 2r.
 This is the formula for the surface area of a sphere, in terms of the radius.
This is the formula for the surface area of a sphere, in terms of the radius.
Add this formula to your list of formulas. You should save your list of formulas to your course folder.
![]() Read
Read
Read “Example 1: Determining the Surface Area of a Sphere” on page 47 to see how the formula A = 4
![]() Self-Check
Self-Check
SC 5. Find the surface area of the following sphere to the nearest square metre.

SC 6. Determine the radius of a sphere with a surface area of 64![]() cm2. Report your answer to the nearest centimetre.
cm2. Report your answer to the nearest centimetre.
![]() Try This
Try This
From the examples, you have learned that you can determine the surface area of a sphere using the formula A = 4![]() r2. You have also seen how the formula can be used to determine the radius of a sphere, if you know the surface area.
r2. You have also seen how the formula can be used to determine the radius of a sphere, if you know the surface area.
Practice what you have learned by completing TT 5 in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson) textbook
TT 5. Complete “Exercises” questions 3.a), 3.c), 8, 9, 13.a), 13.b), and 15 on pages 51 and 52.
Use the link below to check your answers to Try This 5.
There are other ways of determining the surface area of 3-D objects besides analyzing their nets. Often in mathematics, you can discover properties of unfamiliar objects by examining the properties of familiar ones.
For example, the cone is a 3-D object that is shaped much like a pyramid. Like a pyramid, a cone has only one base and the lateral faces of the cone meet at a point called the apex.

The illustration above shows that as you increase the number of sides on the base, the number of faces also increases. The area of each face also becomes smaller.
Eventually, the polygon base approaches the shape of a circle and the lateral area of the pyramid approaches the lateral area of the cone.
You can figure out the formula for the surface area of a cone with this idea in mind.

Consider the formula for the surface area of a rectangular pyramid, as shown in the illustration. The height of the triangular faces, or slant height, is labelled s. The sides of the base are labelled a, b, c, and d.

In the case of a cone, the perimeter of the base is really the circumference of a circle, so its surface area formula would be

![]() Read
Read
Foundations and Pre-calculus Mathematics 10 (Pearson)
![]() Self-Check
Self-Check
Now that you have watched some videos and had a chance to talk with your classmates, it is your turn to try some Self-Check questions to see if you have figured out surface area.

SC 7. When assembled, the net in the preceding illustration will create a
- cube
- cylinder
- cone
- prism
SC 8. Determine the surface area of the following cone to the nearest square foot.

![]() Try This
Try This
Complete the following questions in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. Complete “Exercises” questions 7, 12, and 16.a) on pages 34 and 35.
Use the link below to check your answers to Try This 6.
Connect
Complete the lesson quiz posted under the Assess tab or using the Quizzes link under the Activitites block. Also ensure your work in your binder (course folder) is complete.
![]() Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**
Think about the place that is the focus of your project. What 3-D objects are found in your place? Are there prisms, cones, cylinders, or spheres? If your place is fairly empty of objects, think of the 3-D objects that could occupy your place.
Now go to the Unit 1 Project and complete the Lesson 4 portion of your project.
![]() Going Beyond
Going Beyond

© Pakhnyushcha/shutterstock
Did you know that taller trees generally have more leaves? The water in a tree needs to get from the roots to where photosynthesis happens, which is in the leaves and green parts. If you have a really tall tree, the plant has to force the water against gravity up to its leaves.
How is this possible? Consider the study of surface area. If a plant has large leaves, or numerous smaller leaves, then there is more surface area for evaporation to take place. In a plant, this is called transpiration. When transpiration occurs, the water leaving the plant is replaced by water coming up from the ground—and this water has dissolved nutrients in it.
For more information, initiate an Internet search using the keyword “transpiration” to see what else you can learn about a plant and the surface area of its leaves.
Summary
- How is the concept of surface area applied to understanding the design of structures?
- How do you determine the surface area of a 3-D object?
In this lesson you examined the nets of various 3-D objects. These objects included the prism, pyramid, cylinder, sphere, and cone. From the nets, you were able to determine the surface area formulas for each object. These formulas can be used to determine the surface area of any of the 3-D objects investigated, as long as the required information is given.
Whether you are figuring out how much paint you need to buy or how much wood is needed to build a shed, solving problems involving area comes in very handy.
In the next lesson you will investigate volume, another important concept in design. Then in Lesson 6 you will apply what you have learned about surface area and volume to solve problems.






