Lesson 1: Factors and Multiples
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 1: Factors and Multiples |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:54 AM |
Module 2: Roots and Powers
Lesson 1: Factors and Multiples
Focus

© Monkey Business Images/shutterstock
You will begin this module with a study of prime factors, which are based on prime numbers. A prime number is a whole number greater than 1 whose only factors are 1 and itself.
Factoring numbers is about breaking them down into their parts. Finding the prime factors of a number is when you break a number into its most basic parts—parts that cannot be broken down any further.
As an analogy, think about how you prepare food. You make a cake or an omelette by combining ingredients. The digestion process breaks that food down into its prime components: fats, proteins, and carbohydrates. The food is the whole number and the fats, proteins, and carbohydrates are the prime factors. Also, the ingredients you combine to make the food could be other factors of the food.
With this analogy in mind, look at the following example:
6 × 10 = 60
The ingredients (factors) are 6 and 10, and 60 is the food (whole number).
Break 60 down into key components.
60 = 2 × 2 × 3 × 5
Again, 60 is the food (whole number). Now 2, 3, and 5 are the fats, proteins, and carbohydrates (prime factors).
In this lesson you will learn how to find the prime factors of numbers. You will also investigate how you can use the prime factorization of a number to determine the greatest common factor and lowest common multiple of sets of whole numbers.
Outcomes
At the end of this lesson, you will be able to demonstrate an understanding of factors of whole numbers by
- determining the prime factors of a whole number
- explaining why the numbers 0 and 1 have no prime factors
- determining, using a variety of strategies, the greatest common factor or least common multiple of a set of whole numbers and explaining the process
Lesson Questions
- How are prime numbers important in factoring?
- How is factoring similar to other problem-solving strategies?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. Define a natural number.
2. Define a prime number, and list all prime numbers less than 20.
3. What is meant by the factors of a number?
4. What is meant by the multiples of a number?
5. For the number 24, identify the following:
a. its factors
b. its first four multiples
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
Try the “Prime Number” applet to obtain a definition of prime number. Use the interactive applet to find a four-digit prime number.
Access this “Factor” applet for a definition of factor. You will want to focus on the second definition for factors for natural numbers.
For a more thorough review, watch the interactive piece titled “Multiples, Factors, Primes and Composites” that reviews multiples, factors, and prime numbers. Examine Topics 4, 7, and 10.
Module 2: Roots and Powers
Discover
The Greek mathematician Eratosthenes, who lived in North Africa around 230 BC, invented a simple way of determining prime numbers called the Sieve of Eratosthenes. Complete the Try This to see how this method works.
 Try This 1
Try This 1
Download and print the 100 Grid sheet. Then complete each step.
Step 1: Cross off the number 1 since it is not prime.
Step 2: Circle the number 2, but cross off all multiples of 2 (4, 6, 8, 10, and so on) that are on the grid.
Step 3: Circle the number 3, but cross off all multiples of 3 (6, 9, 12, 15, and so on) that have not already been crossed off on the grid.
Step 4: Look at the next uncrossed number. Circle it and cross off its multiples on the grid.
Step 5: Repeat step 4 until all numbers are either circled or crossed off.
Answer the following questions:
1. How many numbers remain?
2. What do you notice about the numbers that are remaining?
3. How is this method useful?
4. How can you use this method to create a secret code?
Check your answers using the link below.
Module 2: Roots and Powers
Explore

© EdBockStock/shutterstock
Every time you send a credit card number over the Internet, it gets encrypted (converted into code to keep information private) by your browser, and this is based on the theory of prime numbers. In the next section you will further explore prime numbers and how they are used to investigate other numbers.
Glossary Terms
In this lesson the suggested glossary terms you should add to your Glossary Terms include the following:
- composite number
- factor tree
- greatest common factor (GCF)
- lowest common multiple (LCM)
- prime factorization
- prime factors
- prime number
----------------------------------------------------------
 Try This 2
Try This 2
Take the time now to write down the definition of a prime number. You can do an Internet search or take a second look at the “Prime Number” applet at the beginning of the Refresher section.
When you have the definition, answer the following questions:
1. According to the definition of a prime number, is 1 prime? Why or why not?
2. According to the definition of a prime number, is 0 prime? Why or why not?
Use the link below to check your answers to Try This 2.
Module 2: Roots and Powers
Prime Factorization
A number that is not a prime number and has a positive factor other than 1 or itself can be called a composite number. Composite numbers can be expressed as a product of prime numbers. This is called prime factorization.
Example 1
Express the number 60 as a product of prime numbers.
Solution
There are different ways of doing this that all lead to the same result.
The Prime Factorization applet demonstrates how you can use a factor tree to solve this problem. Use the applet to construct a factor tree to help you break 60 into its prime factors.
Depending on how you approached the problem in the example, your factor tree may look different from those of your peers.
Use the applet and the method of factor trees to express the number 144 as a product of primes. Save the factor tree to your course folder.
 Tips
Tips
The usual way of expressing a prime factorization is to write the primes from least to greatest. This way, you can see how many of each factor is required.
Practise your prime factorization skills without using a factor tree.
Play the Prime Number Shooter interactive game a few times and try to beat your own high score! (Make sure to read the instructions before playing).
You can use the prime factorization of a set of numbers to determine the greatest common factor of those numbers. The greatest common factor, or GCF, is the largest number that is a factor of all numbers in the set.
You can also use the prime factorization of a set of numbers to determine the lowest common multiple of those numbers. The lowest common multiple, or LCM, is the smallest number that is a multiple of all numbers in the set.
Example 2
Consider the numbers 48 and 60.
1. Find the GCF.
2. Find the LCM.
Solution
Use prime factorization to express 48 and 60 as products of primes.
48 = 2 × 2 × 2 × 2 × 3
60 = 2 × 2 × 3 × 5
- GCF
Step 1: Identify the factors that both numbers have in common.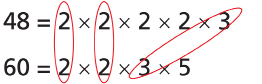
In this case, 48 and 60 have 2, 2, and 3 in common.
Step 2: Multiply the common factors together.
2 × 2 × 3 = 12
The greatest common factor is 12. - LCM
Step 1: Identify the factors that both numbers have in common.
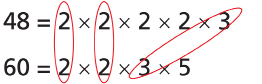
Step 2: Identify factors that are unique to each number. Circle these.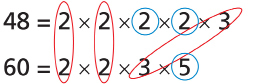
The common factors are 2, 2, and 3.
The unique factors are 2, 2, and 5.
Step 3: Multiply the common factors and unique factors together.
(2 × 2 × 3) × (2 × 2 × 5) = 240
The greatest common factor, or GCF, is the number that contains all the factors common to the numbers in the set. On the other hand, the least common multiple, or LCM, is the smallest number that contains all of the prime factors of each number in the set.
 Tips
Tips
As you practise prime factorization, you may be unsure of whether certain numbers are prime or not. In the Discover section of this lesson, you created a chart of all prime numbers under 100. By referring to this chart, you can check whether a number is prime.
Module 2: Roots and Powers
 Watch and Listen
Watch and Listen
There are other methods of approaching GCF and LCM problems that do not involve prime factorization. The ladder method, for example, can be used to find the LCM and GCF of a set of two, three, or more numbers. Watch the video titled “Ladder Method” to see how this method is used.
Why Does the Ladder Method Work?
You might have seen from the beginning that 24 was the greatest common factor. Dividing both 72 and 120 by 24 would have resulted in 3 and 5, respectively. These last numbers can’t be divided further. Therefore, 6 × 4 is the greatest common factor.
In most cases though, you can also reach the same result by dividing the original numbers by smaller factors. The product of these factors would represent the largest divisor of the original numbers, or the greatest common factor.
In the video, the original numbers were divided by 6 and then by 4. At that point, no other common factors were available. The product of 6 and 4 is 24.
You could have also obtained the same result by dividing the original numbers by 2, then 2, then 2, then 3. Your work would look like this:

Notice here that the GCF is still 24 since 2 × 2 × 2 × 3 = 24.
Example 3
In this example you will learn how to use another method for finding the GCF and LCM of a set of numbers. This method involves listing all the factors and multiples of each number in the set until a match is found.
Consider the numbers 18, 24, and 30.
1. Find the GCF.
2. Find the LCM.
Solution
- GCF
Step 1: List the factors of each number in the set:
-
factors of 18 = 1, 2, 3, 6, 9, 18
-
factors of 24 = 1, 2, 3, 4, 6, 8,12, 24
-
factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
Step 2: To find the GCF, find the largest factor common to all three lists. The answer is 6.
-
- LCM
Step 1: List the first few multiples of the largest number in the set:
- multiples of 30 = 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360, 390
Step 2: Choose the lowest multiple of 30 that is also a multiple of 18 and 24:
- 18 divides into 90, 180, 270, 360, . . .
- 24 divides into 120, 240, 360, . . .
The LCM of 18, 24, and 30 is 360.
 Did You Know?
Did You Know?
Some problems in mathematics cannot be solved by efficient means. Sometimes, problems need to be tackled by checking all cases that could arise. This method is known by many names including the brute force method, proof by exhaustion, or perfect induction. A related method is known as trial and error. Example 3 showed an instance of the use of this method for determining GCF and LCM.
 Try This 3
Try This 3
You have learned several methods for determining the GCF and the LCM of a set of numbers. These include prime factorization, the ladder method, and the method of listing factors and multiples. Which method do you prefer?
Practise using each of these methods to solve some basic problems. You may find that one method works better for you than another, but don’t let that stop you from trying the other methods, too!
Please complete the following exercises in your course folder (binder).
TT 3. Complete “Exercises” questions 8.c, 9.a, c, 10.c, 10.d, 11.a, c, 12 and 13 on page 140.
Use the link below to check your work.
Possible TT3 ( Try This 3 Solutions)
 Self-Check
Self-Check
SC 1. Categorize the following numbers as prime, composite, or neither:
0, 1, 2, 93, 97, 2448
SC 2. Find the GCF for 60 and 75. Explain your reasoning.
SC 3. Find the LCM for 60 and 75. Explain your reasoning.
Finding the GCF and the LCM of numbers can be applied to problem-solving situations. Many problems are multi-step and require some type of plan. An effective way to approach a multi-step problem is to break the problem into smaller steps. This approach is similar to factoring large numbers. Just as you can more readily identify the GCF and LCM of numbers once they have been factored, you can solve a problem more effectively by dividing it into several smaller objectives.
There are many things you need to do when solving problems. Ask yourself exactly what the problem requires. Then determine all the information being given to you in the question. Some key questions to ask include the following:
- What are the key words in the problem?
- Do I need a diagram? A list? A table?
- Is there a formula or equation that I will need? Which one?
- Is there a pattern I can use and/or follow?
- Can I break this problem into a few simpler problems?
As you work through problems, the following chart may help you organize your thinking:
|
Read the Problem |
Explore |
Select a Strategy |
Solve |
Look Back |
|
Note key words. What is known? What is unknown? What are you asked to find? Restate the problem. |
Organize the information. Picture the problem. Draw a diagram or table. Do you know a related problem that could help? |
Here are just a few:
|
Carry out your strategy. |
Check your answer(s). Does it make sense? |
The following example demonstrates how the steps in the chart can be used to approach a problem.
Example 4

© CAN BALCIOGLU/shutterstock
Two buses leave the terminal at 8:00 a.m. Bus A takes 90 minutes to complete its route; bus B takes 75 minutes. When is the next time the two buses will arrive together at the terminal (if they are on time)?
Solution
Read the problem:
Note key words. What is known?
- Bus A takes 90 minutes.
- Bus B takes 75 minutes.
What is unknown? What are you asked to find?
- You need to find out the time when the buses will both be back at the terminal together.
Restate the problem.
- What time will it be when both buses are back at the terminal?
Explore:
Organize the information. Picture the problem. Draw a diagram or table.
In this case, you are working with multiples, so a table makes sense.
|
Bus A |
90 |
180 |
270 |
360 |
450 |
540 |
630 |
|
Bus B |
75 |
150 |
225 |
300 |
375 |
450 |
525 |
Select a strategy:
Here are just a few: pattern recognition, working backwards, guess and check, and reduce or simplify.
For this question, you could use pattern recognition based on the table or you could use prime factorization.
Solve:
Carry out your strategy.
- Method 1: In the table, you can see that after 450 minutes, both Bus A and Bus B will be back at the terminal.
- Method 2: Alternatively, you might choose to use an algebraic method to solve this problem. In this case, you would use one of the strategies learned in this lesson to determine the LCM of 90 and 75.
90 = 10 × 9
= 2 × 5 × 3 × 3
= 2 × 3 × 3 × 5
75 = 3 × 25
= 3 × 5 × 5
Here, the LCM would include all the factors of 90 and those factors of 75 that have not already been taken into account with 90.
LCM = (2 × 3 × 3 × 5) × 5
= 450
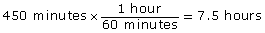
Look back:
Check your answer(s). Does it make sense?
Yes, it seems to make sense. However, the question asks for the time, not the number of hours before the buses meet back at the terminal. If the buses leave at 8:00 a.m., 7.5 hours after 8:00 a.m. is 3:30 p.m. Therefore, the buses will meet at 3:30 p.m.
 Read
Read
Work through an additional example where you can determine the GCF and LCM of a set of numbers to solve a problem.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 4: Solving Problems that Involve Greatest Common Factor and Least Common Multiple” on pages 138 and 139.
 Self-Check
Self-Check
SC 4. What is the side length of the smallest square that could be tiled with rectangles that measure 12 cm × 32 cm? Assume the rectangles cannot be cut. Sketch the square and rectangles.
SC 5. What is the side length of the largest square that could be used to tile a rectangle that measures 12 cm × 32 cm? Assume the squares cannot be cut. Sketch the rectangle and squares.
Module 2: Roots and Powers
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**
Prime numbers play an important role in the creation of secret codes. Some of the most difficult codes to break in the world are based on very large prime numbers. The reason why these codes are tough to break is because there is no quick way to find the prime factors of large numbers. Even modern methods that are used to determine prime factors of large numbers are little better than the brute force method of checking all divisors. In fact, it could take hundreds of years to compute the prime factorization of a thousand-digit number!
Here is an opportunity for you to crack a secret code. In the Discover section of this lesson, you used a chart to determine all the prime numbers less than 100.
Use this chart to uncover a hidden message in the poem:
A green auto
Toward our parking bay
Covered up by bark
From a reeking tree
Towed phoenix sandwiches
Outlandishly by Emma.
For hints, check with your teacher.
At this time, go to the Unit 2 Project and complete the Module 2: Lesson 1 portion of the project.
 Going Beyond
Going Beyond

© markrhiggins/
shutterstock
Codes have long been used to relay messages. In the days of the Cold War, agents from opposing nations tried to prevent enemies from learning military secrets through the use of spy codes.
Today, secret codes continue to be used not only by the military but also by ordinary citizens. Every time you access your online bank account or make an online purchase, you may need to enter a password or code to gain access to private information. There is a whole industry that has evolved that looks strictly at protecting this information. At the same time, criminals continue to develop sophisticated ways of penetrating these security measures and stealing personal information.
Cryptography is the process of storing information in a form that appears scrambled. The original message, known as plaintext, is scrambled using an encryption engine. The engine takes this plaintext and applies information based on prime numbers to create the scrambled message that is called ciphertext. To unscramble the ciphertext, the recipient needs to have access to the key and decryption software.
 Did You Know?
Did You Know?
People have always been interested in keeping secrets. Children’s author Beatrix Potter kept a diary that was written in code. She maintained the belief that the diary would never be read!
Keeping secrets is not new. During World War II, the German forces used a mechanical encryption tool known as the Enigma cipher machine. Search the Internet to learn how this machine worked and how a Polish mathematician named Marian Rejewski was involved with the decryption of Enigma messages.
Module 2: Roots and Powers
Lesson 1 Summary
In this lesson you investigated the following questions:
- How are prime numbers important in factoring?
- How is factoring similar to other problem-solving strategies?
Since prime numbers have no factors other than 1 and themselves, they represent the basic building blocks of the number system. You learned that you can use prime factorization to break a composite number into a product of primes. You can then use those prime numbers to determine the greatest common factor and the lowest common multiple of sets of numbers. You learned multiple methods for determining GCF and LCM besides prime factorization. These include the ladder method and the method of listing factors and multiples. The methods were many, but they were similar because each one involved breaking the numbers into smaller factors.
In this lesson you learned to approach math problems by breaking them down into smaller parts. You can use this approach to tackle other types of problems. For example, in the first unit of this course, you learned to solve trigonometry problems by finding the right triangle in the scenario and then labelling the known and unknown sides and angles. You can also apply this strategy to other types of problems besides those found in a math textbook. Any complicated task such as learning how to drive or planning a birthday party involves smaller steps that all lead to the achievement of the overall task.
In the next lesson you will continue to learn how to use the strategy of breaking down a problem to find square roots and cube roots.





