Lesson 2: Square Roots and Cube Roots
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 2: Square Roots and Cube Roots |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 4:09 AM |
Module 2: Roots and Powers
Lesson 2: Square Roots and Cube Roots
Focus
In the last lesson you discovered how the mathematics of prime numbers are used in the encryption and decryption of codes. One of the best-selling toys since the 1980s is a puzzle that can be easily encrypted, but not so easily decrypted.
The Rubik’s Cube, invented in 1974 by Hungarian sculptor Emo Rubik, is a three-dimensional mechanical puzzle. The classic Rubik’s Cube has six faces, with each face composed of nine smaller panels. These panels are covered with red, orange, yellow, green, white, or blue stickers. The cube is designed so that each face can be pivoted. To encrypt the cube, you must pivot the faces to mix the colours. To decrypt the cube, or to solve the puzzle, the cube must be pivoted until each face is a solid colour again.
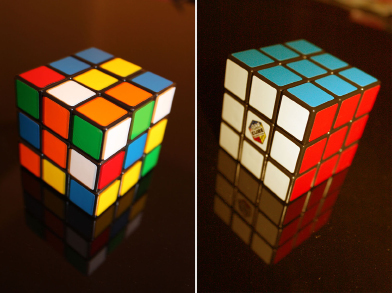
By looking at the photos of the Rubik’s Cube, you can see that each face is composed of 9 smaller cubes. Since it is possible to make a square face out of 9 cubes by placing them in a 3 × 3 arrangement, 9 is considered a perfect square. The square root of 9 is 3 because 3 represents the side length of the square.
You can also see that the entire Rubik’s Cube is composed of 27 smaller cubes. Since it is possible to make a cube out of 27 cubes by placing them in a 3 × 3 × 3 arrangement, 27 is considered a perfect cube. The cube root of 27 is 3 because the cube root represents the side length of the cube.
In this lesson you will learn how to determine whether other numbers are perfect squares or perfect cubes. You will also learn how to calculate square roots and cube roots.
Outcomes
At the end of this lesson, you will be able to
- determine, concretely, whether a given whole number is a perfect square, a perfect cube, or neither
- determine, using a variety of strategies, the square root of a perfect square and explain the process
- determine, using a variety of strategies, the cube root of a perfect cube and explain the process
- solve problems that involve square roots or cube roots
Lesson Questions
- How can you choose the best strategy for determining square roots and cube roots?
- How are square roots and cube roots used to solve real-world problems?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. What is the area of a square with a side length of 6 cm?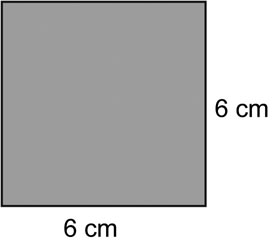
2. What are the dimensions of a square with an area of 81 ft2?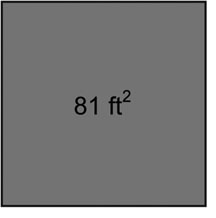
3. Complete the table.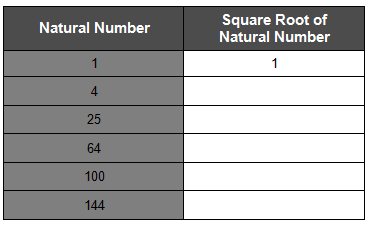
4. Express the following numbers as a product of primes:
a. 24
b. 90
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
How did you do? Did you remember the relationship between the length of a square and its area?
If you are not completely sure about square roots, have a look at the “Square Roots” applet. It provides a definition and example of square roots, as well as a method of how to estimate a square root.
Go to “Exploring Square Roots,” where you can drag sliders to determine the length of a side of a square. This allows you to see the relationship between the area of a square (a number) and the length of the side of the square (the square root of the number). Experiment with the image by dragging the slider to increase or decrease the area.
Materials
- Grid Paper (either electronic or paper)
You will also require these materials to complete Math Lab: Manipulatives.
- 150 counters or pennies
- 150 unit blocks or sugar cubes
Module 2: Roots and Powers
Discover
Recall the method of prime factorization from the previous lesson. Use this method to complete the Try This investigation.
 Try This 1 - 4
Try This 1 - 4
TT 1. Complete Steps 1 to 3 for the number 36.
Step 1: Generate the prime factorization for the number.
Step 2: Rearrange the prime factors into two identical groups.
Step 3: Evaluate the product of the factors in each group.
TT 2. Repeat Steps 1 to 3 for the following numbers:
a. 81
b. 144
TT 3. Generate the prime factorization for the following numbers:
a. 30
b. 56
TT 4. Can you rearrange the prime factors of these numbers into identical groups as you did for the numbers in TT 1 and TT 2? Explain.
Use the link below to check your answers to Try This 1 - 4.
Possible TT1-4 (Try This 1-4) Solutions
 Share
Share
Discuss your results with a classmate or in a group ( if possible) . In your discussion, address the following questions:
1. What is the difference between the numbers examined in TT 1 and TT 2 and the numbers in TT 3 and TT 4?
2. In Step 3, how is the product of the factors in each identical group related to the original number?
3. a. How can you use prime factorization as a method to determine that a number is a perfect square?
b. How can you use prime factorization as a method to determine the square root of a number?
Save a copy of your revised work in your course folder ( binder). You will be referring to these results in a later part of the lesson. If you do not have access to another student, or an appropriate partner with whom to share your work, use the provided answers below to check your work.
Module 2: Roots and Powers
Explore
Do you know the name of the famous celebrity portrayed in this artwork? It is composed of more than 400 Rubik’s Cubes! A special property of the number 400 is that it is a perfect square. In this lesson you will continue to explore perfect squares and perfect cubes, and you will investigate how you can find their roots.

Cube Works Studio, Toronto.
Glossary Terms
Add the following terms to your "Glossary Terms" section in your notes.- cube root
- perfect cube
- perfect square
- square root
------------------------------------------------
A perfect square is any whole number that can be represented as the area of a square with a whole number side length. The length of the square is the square root. For example, imagine a piece of art like the one in the photograph is made out of 256 Rubik’s Cubes. The number 256 is a perfect square since a square with an area of 256 square units has a side length of 16 units, a whole number. On the other hand, while it is possible to have a square with an area of 300 square units, the side length of the square would not be a whole number.
Similarly, a perfect cube is any whole number that can be represented as the volume of a cube with a whole number side length. The length of the cube is the cube root. For example, the number 8 is a perfect cube since a cube with a volume of 8 cubic units has a side length of 2 units, a whole number.
There are many ways to determine if a number is a perfect square or a perfect cube:
- manipulatives and diagrams
- prime factorization
- guess and check
- calculator
 Math Lab: Manipulatives
Math Lab: Manipulatives
Complete Math Lab: Manipulatives in your course folder ( binder). The lab will help you identify perfect squares and perfect cubes by using manipulatives to build squares and cubes. Before you begin, print (or copy by hand) a copy of Perfect Squares and Perfect Cubes Data Sheet.
Materials
- 150 counters or pennies
- 150 unit blocks or sugar cubes
- printed copy of data sheet – Perfect Squares and Perfect Cubes Data Sheet
Procedure
The following steps assume you are using pennies and sugar cubes, but you could also use counters and unit blocks respectively.
Step 1: Arrange the pennies or sugar cubes into squares with different side lengths. Record the total number of pennies or cubes used for each square in the first table on the data sheet.
Analysis
Answer the following questions:
1. Which numbers less than 150 are perfect squares?
2. Which numbers less than 150 are perfect cubes?
3. How could you use a sheet of graph paper, instead of counters or pennies, to do Step 1 in the procedure?
4. What other methods could you use to determine whether a number is a perfect square or a perfect cube?
Use the link provided below to check your answers
Math Lab: Manipulatives Answers
____________________________________________________________________
Diagrams
If you are going to draw diagrams, it really helps if you have graph paper available. Also, the diagram method works best for smaller numbers; you don’t really want to draw a diagram to figure out if 4096 is a square number! For large numbers, you may want to begin with the guess and check method.
If you were asked if 196 was a square number, you could pull out your graph paper and begin counting 196 squares, remembering the shape you draw must be a square. (Each side must be the exact same length.)
This diagram has 196 squares and it is a square shape, so you know that 196 is a perfect square.

To find the square root of 196, find the length of each side.
Each side is 14 units long, so 14 × 14 = 196. The square root of 196 is 14.
Prime Factorization
Another way you can identify perfect squares and perfect cubes is to use prime factorization.
Recall your data from the Math Lab in this lesson. You were asked to express 144 as a product of primes. Your result should have looked like this:
144 = 2 × 2 × 2 × 2 × 3 × 3
You can rearrange the prime factors into two identical groups:
144 = (2 × 2 × 3) × (2 × 2 × 3)
This result can be simplified:
144 = 12 × 12
This means that you can use 144 pennies to create a square with a side length of 12. In other words, 144 is a perfect square with a square root of 12.
Module 2: Roots and Powers
 Read
Read
Go to the textbook and work through the following examples to see how prime factorization is used to identify numbers as perfect squares or perfect cubes. This method also helps you to determine the square roots and cube roots of those numbers. As you read, focus on how the prime factors are regrouped into identical groups to find the square and cube roots.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Determining the Square Root of a Whole Number: Method 1” on page 144 and “Example 2: Determining the Cube Root of a Whole Number: Method 1” on page 145.
 Self-Check
Self-Check
SC 1. Use prime factorization to determine whether the number 3375 is a perfect square, a perfect cube, or neither. If it is a perfect number, state the square root or cube root.
You may wish to use the applet “Prime Factorization” you used in Lesson 1.
SC 2. Identify each of the following numbers as a perfect square, a perfect cube, both, or neither: 16, 125, 64, 32.
Guess and Check
Guess and check can be a very useful method in math, especially if you are re-examining your choice after each guess so you can get closer and closer to the answer.
You might be asked to find out if 1728 is a perfect cube. Here is one way you can use guess and check:
10 × 10 × 10 = 1000
You need 1728, which is greater than 1000, so you need a number greater than 10.
13 × 13 × 13 = 2197
You need 1728, which is less than 2197, so you need a number less than 13 and greater than 10.
12 × 12 × 12 = 1728
Therefore, 1728 is a perfect cube since its cube root is 12.
What if the number is not a perfect cube? What would your guess and check look like? If you were asked if 340 was a perfect cube, you would go though similar calculations:
10 × 10 × 10 = 1000
You need 340, which is less than 1000, so you need a number less than 10.
5 × 5 × 5 = 125
You need 340, which is greater than 125, so you need a number greater than 5.
7 × 7 × 7 = 343
You need 340, which is less than 343, so you need a number less than 7.
6 × 6 × 6 = 216
You need 340, which is greater than 216, so you need a number greater than 6.
Uh-oh. So you find you need a number greater than 6 but less than 7. How is that possible? Well, it means your answer will be a decimal number between 6 and 7.
Therefore, 340 is not a perfect cube since its cube root is a decimal number.
Calculator Method

© Dirk Herzog/shutterstock
While you could continue with the guess-and-check method to find the cube root of 340, a faster way would be with a calculator.
Example 1
Evaluate 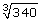 with your calculator. Round your answer to 4 decimal places.
with your calculator. Round your answer to 4 decimal places.
Solution
The keystrokes will vary depending on your calculator. Consult your calculator menu for the keystrokes appropriate for your calculator. Two possible sequences are provided here.
scientific calculator:

graphing calculator: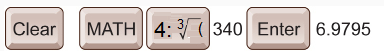
or

 Read
Read
There are multiple methods for finding square roots and cube roots. In fact, there are even variations of the same method! Go to the textbook and read the following examples. Can you find the differences in the ways these methods are presented in the lesson compared to the textbook examples?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Determining the Square Root of a Whole Number: Method 2” on page 144 and “Example 2: Determining the Cube Root of a Whole Number: Method 2” on page 145.
Can you identify the key thinking in this approach to estimation that helps you to narrow your search for the solution?
You have learned how to identify and determine square roots and cube roots. Now you can begin to apply those strategies to solving problems. As you do so, recall the chart that helps you to organize and plan your approach to these problems.
|
Read the Problem |
Explore |
Select a Strategy |
Solve |
Look Back |
|
Note key words. What is known? What is unknown? What are you asked to find? Restate the problem. |
Organize the information. Picture the problem. Draw a diagram or table. Do you know a related problem that could help? |
Here are just a few:
|
Carry out your strategy. |
Check your answer(s). Does it make sense? |
Example 2
A cube can hold 729 cm3 of sand. Show how you could use two different strategies to calculate the length of its side.
Solution
Since it is a cube, you know all sides (length, width, and height) are the same. So, you need a number that can multiply by itself three times to get 729.
729 = side × side × side
Strategy 1: Guess and Check
|
6 × 6 × 6 = 216 |
So you know you need a number more than 6. |
| 10 × 10 × 10 = 1000 | So you know you need a number less than 10. |
| 9 × 9 × 9 = 729 | So you have it! |
Strategy 2: Prime Factorizaton
You can also use the prime factorization method to find the cube root of 729.
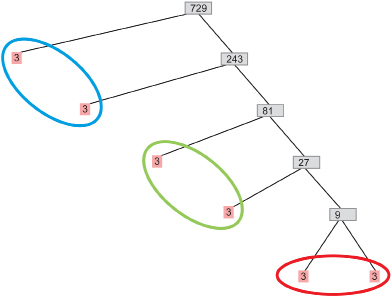
There are three groups of 3 × 3, so you can write 729 as 93.
Strategy 3: Using a Calculator
If you are not a fan of trial and error, you could also find the cube root of 729.
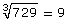
So this means 9 × 9 × 9 = 729.
 Self-Check
Self-Check

© Suzanne Tucker/shutterstock
SC 3. Adam wants to make some extra money over the summer, so he decides to mow lawns. His neighbour has a square lawn with an area of 576 ft2.
- What are the dimensions of his neighbour’s square lawn?
- As Adam collects the grass clippings, he adds them to his plastic cube bin. The bin has a volume of 7415 in3. What are the dimensions of the cube bin to the nearest tenth of an inch?
SC 4. Can a negative number be a perfect square? Can it be a perfect cube? Explain your answers.
 Try This 5
Try This 5
Practise applying the concepts of square roots and cube roots to these problems in your textbook. Read the questions carefully as they may require you to do more than one step.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 5. Complete “Exercises” questions 4.b), 5.c), 6.b, 6.d), 9, 11and 14 on pages 146 and 147.
Use the link below to check your answers to Try This 5.
Possible TT5 (Try This 5) Solutions
 Did You Know?
Did You Know?
Square Root Day occurs when the month number and date are square roots of the last two digits of the year. For example, 3/3/2009 was a Square Root Day. The next Square Root Days will be on 4/4/2016 and 5/5/2025. There are only nine Square Root Days each century, so they are even more rare than leap days!
Module 2: Roots and Powers
 Lesson Assessment
Lesson Assessment

© Chris Harvey/shutterstock
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED **
Project Connection **NOT ASSIGNED **
A cipher is a procedure for encrypting or decrypting secret messages. One way to encode a message is by using a substitution cipher where each letter in the message is substituted by a number.
Retrieve your grid of the prime numbers less than 100 from Lesson 1. Notice that there are 25 primes less than 100. Since there are 26 letters in the alphabet, you can choose a letter to be unassigned (for example, you could leave Q unassigned and use K when your code calls for a Q) or you could make use of the next prime number (greater than 100), which is 101.
Using this last method, your table of substitutions looks like this:
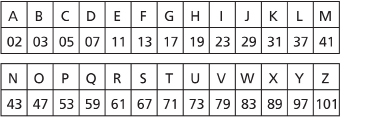
You can use this method to encode the expression “I LOVE MATH.”
Step 1: Use the table to determine the corresponding prime number substitutions for each letter in the code.
23 37 47 79 11 41 02 71 19
Step 2: Write the numbers together.
233747791141027119
(By writing the numbers together, you can hide the fact that each number represents a letter.)
You can also use this method to decrypt the code: 410271192367137343.
Step 1: Break the code into pairs of digits.
41 02 71 19 23 67 13 73 43
Step 2: Use the table to determine the corresponding letter substitutions for each prime.
M A T H I S F U N
Step 3: Use reasoning to determine where the words begin and end.
MATH IS FUN
The problem with substitution ciphers is that they are easy to figure out. A person could use letter frequencies to break the code. In the first two lessons of this module, you used prime factorization to determine GCF, LCM, square roots, and cube roots. How can you use prime factorization as a cipher?
Encode the expression “I LOVE MATH.”
Step 1: Break the phrase into three-letter blocks.
ILO VEM ATH
Step 2: For each block of letters, multiply the prime number substitutions together.
ILO = 23 × 37 × 47 = 39997
VEM = 79 × 11 × 41 = 35629
ATH = 2698
This is the first part of your code.
Step 3: Think: If the three letters in each block were to be arranged in alphabetical order, which one would be first, second, and last? Assign each letter a number from 1 to 3 depending on the position of the letter in an alphabetical arrangement of the letters.
ILO = 123
VEM = 312
ATH = 132
This is the second part of your code.
Step 4: Put the first and second parts of the code together.
39997-123
35629-312
2698-132
5822-213
You can decrypt the code 29279-123 by following this procedure:
40807-132
Step 1: Perform the prime factorization of the first part of each number. Since the numbers are large, you may want to use the prime factorization applet used in this lesson to simplify the calculations. Write the factors initially in order from least to greatest.
5822 = 2 × 41 × 71
29279 = 19 × 23 × 67
40807 = 13 × 43 × 73
Step 2: Rearrange the factors of each number in the order described by the second part of each number.
Since the sequence for 5822 is 213, this means the correct arrangement of factors in the prime factorization is the second factor, then the first factor, and then the third factor.
5822 = 41 × 2 × 71
Similarly, for 29279, since the second part is 123, this means to write the first factor first, the second factor second, and the third factor last.
29279 = 19 × 23 × 67
40807 = 13 × 73 × 43
Step 3: Write all the factors together.
41 2 71 19 23 67 13 73 43
Step 4: Use the grid to convert the primes into letters.
M A T H I S F U N
The message is “MATH IS FUN.”
Reflect on these questions:
- Why were the letters put into three-letter groups before encoding? What would happen if the message was not broken into smaller groups of letters?
- Why is it necessary in this method to add an extra three digits at the end of the number?
- How is the cipher based on prime factorization more difficult to break than the substitution cipher originally introduced?
At this time, go to the Unit 2 Project and complete the Module 2: Lesson 2 portion of the project.
 Going Beyond
Going Beyond
In this lesson you used the method of prime factorization to determine the square roots and cube roots of natural numbers. Fortunately, those natural numbers were small enough that they could be factored in a relatively short amount of time.
There are certain tests that you can perform to quickly know whether a natural number, n, is divisible by other numbers. For example, you may know that n is divisible by 2 if n is even. You may also know that n is divisible by 10 if the last digit is 0.
Use reasoning and search the Internet to discover what the tests of divisibility are for the numbers from 2 to 10. You may want to use the search terms “tests of divisibility.”
|
Divisor |
Test |
|
2 |
If the last digit is even, then the number is divisible by 2. |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
Use your reasoning ability to determine what tests of divisibility may exist for other numbers. How can knowing whether a number, n, is divisible by a greater number help you in prime factorization?
Module 2: Roots and Powers
Lesson 2 Summary
In Lesson 2 you investigated the following questions:
- How can you choose the best strategy for determining square roots and cube roots?
- How are square roots and cube roots used to solve real-world problems?
In this lesson you learned how to find the square root and cube root of a number using several methods: manipulatives and diagrams, guess and check, prime factorization, and using a calculator. The strategy you choose to solve a particular problem will depend on a number of factors including the materials you have on hand, the size of the numbers in the problem, and your own preferences. If you have graph paper, for instance, you may opt to use diagrams to model the problem. On the other hand, this method may not be appropriate if the numbers in the problem are larger than the number of grid squares on the graph paper. In this case, prime factorization or the use of a calculator may be more suitable.
Square roots are most often seen in the solutions of area problems, while cube roots are used in the solution of volume problems. In this lesson you learned how to tell if a number is a perfect square or a perfect cube. In a subsequent lesson you will use this information to explore radicals.

