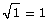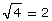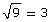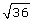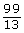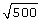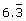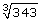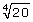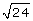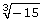Lesson 3: Irrational Numbers
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 3: Irrational Numbers |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:55 AM |
Description
Created by IMSreader
Module 2: Roots and Powers
Lesson 3: Irrational Numbers
Focus

left: © PictureLake/1053965/Fotolia (Mona Lisa); right: © Roman Rudyak/shutterstock (building)
In this lesson you will encounter a classification of numbers known as irrational numbers. Some examples of irrational numbers include ![]() (pi) and
(pi) and 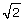 , or Pythagoras’ constant. Irrational numbers have been used in mathematics to describe lengths and the ratios of certain lengths. For example, pi is an irrational number that represents the ratio of a circle’s circumference to its diameter. Similarly,
, or Pythagoras’ constant. Irrational numbers have been used in mathematics to describe lengths and the ratios of certain lengths. For example, pi is an irrational number that represents the ratio of a circle’s circumference to its diameter. Similarly, 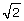 is the length of the diagonal of a square with side lengths equal to one unit.
is the length of the diagonal of a square with side lengths equal to one unit.
Irrational numbers are also used in art and design. The golden ratio is a geometric proportion long thought to be the most aesthetically pleasing to the eye. You can find the golden ratio in the design of the Parthenon in Athens and in Leonardo da Vinci’s celebrated Mona Lisa, as well as other celebrated artwork and structures.
At the end of this lesson you will see how the properties of irrational numbers are well suited to code construction. You will also have the opportunity to use irrational numbers to create your own cipher.
Outcomes
At the end of this lesson, you will be able to demonstrate an understanding of irrational numbers by
- representing, using a graphic organizer, the relationship among the subsets of the real numbers (natural, whole, integer, rational, irrational)
- sorting a set of numbers into rational and irrational numbers
- determining the approximate value of an irrational number
- approximating the locations of irrational numbers on a number line, using a variety of strategies, and explaining the reasoning
Lesson Questions
- How are irrational numbers different from rational numbers?
- How are the properties of irrational numbers suited to code construction and other applications?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. Place the following numbers on a number line from least to greatest: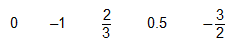
2. Complete the table that shows how rational numbers can be converted from fraction form to decimal form.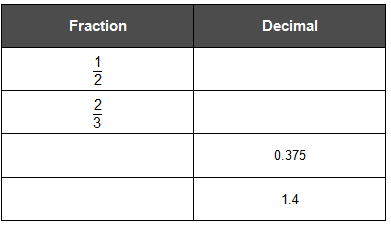
3. What is the difference between a whole number and a rational number?
4.Classify the following numbers as
- natural numbers
- whole numbers
- integers
- rational number
In most cases a number will belong to more than one category. Write the number in all categories that apply.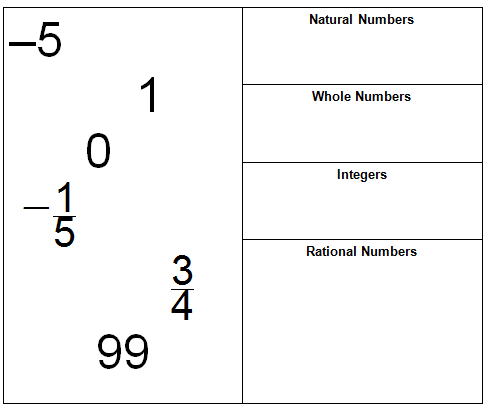
5. Use your calculator to evaluate the following expressions to 5 decimal places.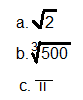
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
You will be learning how to place irrational numbers on a number line in this lesson. This “Number Line” applet will remind you of the basics of a number line. See if you can use the applet to insert fractions and decimals as well as integers—both positive and negative—on the number line.
Use the “Rational Numbers” applet to review the definition of a rational number. You should also review the subsets of the rational numbers, including naturals, wholes, and integers. Use the applet to see examples of numbers included and not included in each number set.
Module 2: Roots and Powers
Discover
In the Discover section of the previous lesson you looked at how you could rearrange the prime factors of given numbers. In doing so, you discovered you could identify perfect squares and perfect cubes. You could also determine the square roots and cube roots of those numbers.
The Discover section in this lesson is again based on prime factorization. This time you will focus on the number of prime factors possessed by perfect squares.
 Try This 1 - 4
Try This 1 - 4
Complete the following questions in your course folder ( binder).
TT 1. Determine the prime factorization of the following numbers:
6, 12, 20, 25
TT 2. Now determine the prime factorization of the squares of the numbers in TT 1.
TT 3. Form a hypothesis for the number of prime factors in the prime factorization of perfect squares.
TT 4. Test your hypothesis with other perfect squares. Can you find a counterexample?
Use the link below to check your answers to Try This 1- 4.
Possible TT1-4 (Try This 1-4) Solutions
Module 2: Roots and Powers
Explore

© John R. Smith/shutterstock
Computer manufacturers have many ways of testing the strength of the computers they make. One way they do this is with software that enables a computer to evaluate the constant pi to a large number of decimal places. If the computer can correctly evaluate pi to a predetermined number of decimal places—usually in the millions—then it has shown that it can perform billions of calculations without an error.
Glossary Terms
Add the following terms to your "Glossary Terms" page:
- graphic organizer
- irrational number
- nested diagram
- rational number
-----------------------------------------------------------
Rational numbers are part of the real number system. Any number that can be written as a fraction is considered rational. More specifically, rational numbers can be expressed in the form 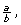 where a and b are integers
where a and b are integers 
 Caution
Caution
It is not possible to evaluate division by zero since the answer is undefined. You can think about it this way:
When you are asked to evaluate 6 ÷ 2, you must determine how many groups of 2 objects you must gather to have a total of 6 objects. The answer is 3 groups.
When you are asked to evaluate 24 ÷ 6, you must determine how many groups of 6 objects you must gather to have a total of 24 objects. The answer is 4 groups.
However, when you are asked to evaluate 2 ÷ 0, you must determine how many groups of 0 you must gather to have a total of 2 objects. In this case, it is impossible to gather enough groups of 0. No matter how many groups you gather, you will still have nothing. Therefore, division by 0 is considered undefined.
All integers are examples of rational numbers since any integer can be written as a fraction by adding a denominator of 1.
For example, both 10 and −10 are integers. These integers can be expressed as the fractions 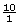 and
and 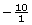 , respectively.
, respectively.
Decimals are rational numbers as long as their digits terminate or repeat. For example, the following decimals are rational:
6.12 −30.8924 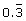
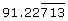
So what is an irrational number?
Irrational numbers include all those numbers that are not rational numbers. These are the numbers that cannot be written in the form 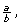 where a and b are integers
where a and b are integers 
Practically speaking, you can think of irrational numbers as decimals that neither terminate nor repeat.
For example, ∏ is 3.141 592 6 . . . . Even though ∏ has been calculated to over 1 trillion decimal places, a pattern in the digits has not been discovered.

Other examples of irrational numbers include the square root of certain numbers.
If the sides of the triangle are each equal to 1 as seen in the diagram, then according to the Pythagorean Theorem, 12 + 12 = 2, so that the hypotenuse is 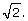 Since there is no rational number whose square is 2,
Since there is no rational number whose square is 2, 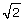 is therefore an irrational number.
is therefore an irrational number.
What about the square root of other natural numbers?
|
|
|
|
|
|
|
|
|
|
|
|
Do you notice which kinds of numbers in the table are rational and which ones are irrational?
The information in the table suggests that square roots of numbers that are not perfect squares are, in fact, irrational. One way to prove this statement is shown in the video clip titled “Root 2 Proof” in the Watch and Listen section.
 Caution
Caution
Since a calculator has a limited amount of space across its screen, it is not the best way to determine whether a number is irrational. For example, 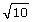 appears as 3.16227766 on some calculators. Since it appears to be a terminating decimal, you might incorrectly assume it is irrational. The best way to know whether the square root of a number is irrational is to figure out whether the number is a perfect square.
appears as 3.16227766 on some calculators. Since it appears to be a terminating decimal, you might incorrectly assume it is irrational. The best way to know whether the square root of a number is irrational is to figure out whether the number is a perfect square.
Module 2: Roots and Powers
 Watch and Listen
Watch and Listen
Retrieve your work from Try This 1 - 4. Did you learn that the prime factorization of a perfect square would always result in an even number of prime factors? Confirm this statement by looking at your results and conclusion. For example, the prime factorization of 144 is
144 = 2 × 2 × 2 × 2 × 3 × 3
The number 144 has six prime factors—an even number of factors—in its prime factorization.
An integer will have either an odd number or an even number of prime factors.
A perfect square will have twice as many prime factors in its prime factorization compared to its square root. Since you will always get an even number when you double any number, whether odd or even, a perfect square will always have an even number of factors in its prime factorization.
View the video titled “Root 2 Proof” to see how you can use this discovery to prove that 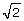 is irrational.
is irrational.
The video shows just one way you can prove 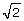 is irrational. Generally, the square root of a number that is not a perfect square is irrational.
is irrational. Generally, the square root of a number that is not a perfect square is irrational.
Similarly, the cube root of a number that is not a perfect cube is irrational.
Use the “Real Numbers” applet to review the differences between rational and irrational numbers. Study the nested diagram of Number Systems carefully and pay special attention to the examples given for both sets of numbers. You will need to recall this diagram later in the lesson.
So far in this lesson, you have learned that a rational number can always be written in the form 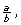 where a and b are integers
where a and b are integers 
In decimal form a rational number is either terminating or repeating.
An irrational number cannot be expressed in the form 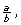 where a and b are integers
where a and b are integers 
In decimal form an irrational number neither terminates nor repeats. Rather, an irrational number continues indefinitely with no periodic pattern in its digits.
The non-terminating and non-repeating nature of irrational numbers makes it ideally suited for code construction. If you have constructed a code that requires a key or password to access, you can use a sequence of digits from an irrational number. Better yet, you can multiply two irrational numbers together to get a third irrational number and use any sequence of digits of that number as your key. If your code is intercepted, the only way it can be broken is if the intruder knows the two irrational numbers and also knows which sequence of digits to look for. Otherwise, the key looks just like a series of patternless digits!
 Self-Check
Self-Check
SC 1. Classify the numbers as rational numbers or irrational numbers. Give your reasons for the classification.
|
Number |
Rational/Irrational |
Reason |
|
0 |
||
|
|
||
|
|
||
|
− 4.2558 |
||
|
− 4.2558 . . . |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Now that you have determined how to identify irrational numbers, you can investigate how to locate irrational numbers on a number line. There are many strategies for doing this, with each strategy having its own advantages and drawbacks.
For example, one of the easiest ways to locate an irrational number on a number line is by using a calculator. However, a calculator can only give you an approximation of where a root might be located. As you read the next example, consider the advantages and drawbacks of each method.
Example 1
Use different strategies to locate the number 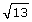 on a number line.
on a number line.
Method 1: Calculator
Step 1: Evaluate![]()
![]()
Step 2: Draw a number line.
Step 3: Insert the irrational number on the number line.
Since ![]() is slightly more than halfway between 3 and 4, it looks like this:
is slightly more than halfway between 3 and 4, it looks like this:
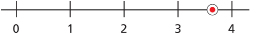
Method 2: Approximation Using Benchmarks
Think about the first few perfect squares:
|
Natural Number |
Square |
|
1 |
1 |
|
2 |
4 |
|
3 |
9 |
|
4 |
16 |
These numbers can be used as benchmarks to help you obtain a more accurate estimate.
Since 9 < 13 < 16, then 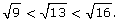
In other words, 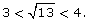
Since 13 is a little closer to 16 than it is to 9, you can reason that 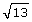 is closer to 4 than it is to 3. A good guess might be 3.6 or 3.7.
is closer to 4 than it is to 3. A good guess might be 3.6 or 3.7.
Draw a number line with the point at approximately 3.6 (or 3.7).
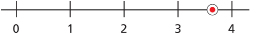
Method 3: Using a Compass and Straightedge
 Watch and Listen
Watch and Listen
You can locate an irrational number more accurately with a compass and straightedge. Watch "Root 13 Construction" to see how this can be done.
 Try This 5
Try This 5
TT 5. Complete the following questions in your course folder ( binder).
1. a. Compare and contrast the three methods used to locate an irrational number on the number line. Organize your ideas in the table.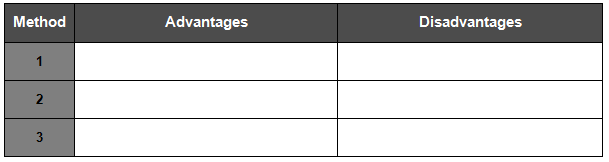
b. Which method do you prefer? Give your reasons.
c. In what situations would you use each method? In what situations would each method be inappropriate?
d. What other methods could be used to locate an irrational number on the number line?
 Share
Share
Compare your answers with another classmate or appropriate partner ( if possible). Record any similarities and differences you discussed in your course folder (binder).
 Did You Know?
Did You Know?
One form of high-level encryption depends on an unlimited source of patternless digits. This is an innovative application of irrational numbers.
 Self-Check
Self-Check
SC 2. Place the following irrational numbers on a number line:
SC 3. Use the methods of locating irrational numbers to arrange the following irrational numbers on a number line:
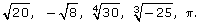
 Try This 6
Try This 6
Complete the questions from your textbook in your course folder ( binder) to help you identify rational and irrational numbers and place them on a number line. Use your calculator to check that your result is accurate.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. Complete “Exercises” questions 3 and 12 on page 211.
Use the link below to check your answers to Try This 6.
Module 2: Roots and Powers
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete. .
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**
How do you create a cipher based on irrational numbers? Read the following introduction to substitution ciphers with shifts. Then examine an application of this cipher system using irrational numbers.
In cryptography, the term plaintext refers to the letters in the message, whereas the term ciphertext refers to the letters or numbers after the message has been encrypted. You have already seen what a substitution cipher looks like. Here is another version that does not use prime numbers. The following table is called a cipher strip.
![]()
In this case, the message “SECRET CODE” would be encrypted as follows:
18 4 2 17 4 19 2 14 3 4
This code would be easy to break as soon as you recognize that each number represents the position of each letter in the alphabet relative to A. So, the ciphertext that corresponds to the letter C is 2 because C is two letters away from A. You can make the code a little tougher to break by shifting the numbers along the bottom.
You can make the code a little tougher to break by shifting the numbers along the bottom.
![]()
Now the message “SECRET CODE” would be encrypted as follows:
19 5 3 18 5 20 3 15 4 5
Since a would-be code breaker would not know how the second row is shifted, the task of breaking the code becomes more difficult. To make the code even more difficult to break, you could introduce a different shift for every letter of the message. To do this, first create an extended cipher strip that includes at least ten possible shifts.
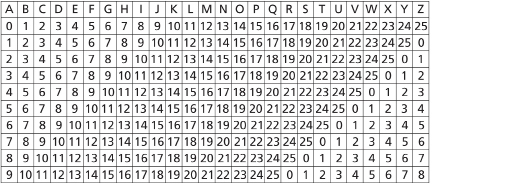
This table shows only ten shifts, but it could be extended for up to twenty-five different shifts.
You can use this block of data to create a cipher based on irrational numbers. The main feature of an irrational number is the fact that it presents an unending source of patternless digits. You can use this to your advantage when creating a cipher.
Follow these steps to encode a secret message:
Step 1: Choose an irrational number. This is the key.
Let ![]() be the key.
be the key.
Step 2: List the digits of the irrational number beyond the decimal point:
![]()
So, the digits of ![]() beyond the decimal point are 141592653589793238 . . . .
beyond the decimal point are 141592653589793238 . . . .
Step 3: Write the digits below each of the letters in your message. You will only use as many digits as you need.
If you want to encode the message “SECRET CODE,” then write
![]()
Step 4: Use the number under each letter as the shift required to encode the letter.
- Since S has a shift of 1, it is encoded as 19. (Look at where the number 1 in the first column and E across the top row intersect.)
- Since E has a shift of 4, it is encoded as 8.
- Since C has a shift of 1, it is encoded as 3.
- Since R has a shift of 5, it is encoded as 22.
- Since E has a shift of 9, it is encoded as 13.
- And so on . . .
The completed cipher text is written as follows:
19 8 3 22 13 21 8 19 6 9
Notice that although there are two values of 19 in the cipher text, each one actually represents a different letter! Also notice that although there are three instances of the letter E in the message, each one is represented by a different number!
Reflect on these questions:
- What are the steps for decoding a secret message using the cipher just explained? Use
 as the key to decode the ciphertext 3 4 5 23 9 19 into plaintext. (The result is the name of someone who was the first to use substitution ciphers with shifting.)
as the key to decode the ciphertext 3 4 5 23 9 19 into plaintext. (The result is the name of someone who was the first to use substitution ciphers with shifting.) - What are the benefits and drawbacks of this cipher?
At this time, go to the Unit 2 Project and complete the Module 2: Lesson 3 portion of the project.
 Going Beyond
Going Beyond
Phi, 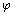 , is an irrational number that is sometimes known as the golden ratio, the golden mean, and the divine proportion.
, is an irrational number that is sometimes known as the golden ratio, the golden mean, and the divine proportion.
The value of phi (pronounced fee) is given the mathematical expression 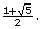 The decimal equivalent of this expression begins with 1.618 03 . . . .
The decimal equivalent of this expression begins with 1.618 03 . . . .
Although less celebrated than pi, phi is nevertheless a special number.
In Dan Brown’s book entitled The Da Vinci Code, professor Robert Langdon tells a class of university students:
“Nobody understood better than Da Vinci the divine structure of the human body. Da Vinci actually exhumed corpses to measure the exact proportions of human bone structure. He was the first to show that the human body is literally made of building blocks whose proportional ratios always equal phi.”
Everyone in class gave him a dubious look.
“Don’t believe me?” Langdon challenged. “Next time you’re in the shower, take a tape measure.”
Dan Brown. The Da Vinci Code Special Illustrated Edition. New York, Doubleday, 2003. p. 100.
Make a chart similar to the one that follows. Ask someone to help you measure the following lengths of your body. Then divide Measurement A by Measurement B in each row to obtain the ratio.
|
Measurement A |
Measurement B |
Ratio of Measurement |
|
tip of head to floor |
belly button to the floor |
|
|
shoulder to fingertips |
elbow to fingertips |
|
|
hip to floor |
knee to floor |
|
|
fingertips to elbow |
wrist to elbow |
Answer the following questions:
- Look at the ratios in the final column. How close are they to
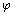 ?
? - Complete the chart of body measurements again by taking the measurements of a friend, classmate, or relative. How close are his or her results to
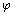 ?
? - Conduct an Internet search to find out what other aspects of the human body relate to
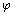 . Use the search terms “golden section” and “divine proportion.” What other ratios did you find out are close to
. Use the search terms “golden section” and “divine proportion.” What other ratios did you find out are close to 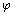 ?
?
Suggestions for further investigation:
- Borrow the book The Da Vinci Code by Dan Brown from your local library and read Chapter 20 to see what other examples Professor Langdon gives regarding the manifestation of
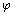 in nature.
in nature. - Conduct an Internet search to see how
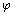 was originally discovered. Use the search terms “phi,” “golden mean,” and “divine proportion.”
was originally discovered. Use the search terms “phi,” “golden mean,” and “divine proportion.”
Module 2: Roots and Powers
Lesson 3 Summary
A graphic organizer is a visual display that is used to depict the relationships between facts, terms, and/or ideas within a learning task. It forms a powerful visual picture of the information that allows the mind to discover patterns and relationships it otherwise may have missed.

Have you ever seen a set of Russian nested dolls like the ones in the photo? You open up the first one by separating the top half of the doll from the bottom half only to find a second doll nested inside. When you open up the second doll, you find a third doll inside. As this continues, the dolls become smaller and smaller until the smallest doll is found with the same proportions as the original. The real number system can be represented in this same nested fashion.
In Lesson 3 you investigated the following questions:
- How are irrational numbers different from rational numbers?
- How are the properties of irrational numbers suited to code construction and other applications?
You have learned that a rational number can always be written in the form 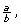 where a and b are integers
where a and b are integers 
In decimal form, a rational number is either terminating or repeating.
An irrational number cannot be expressed in the form 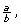 where a and b are integers
where a and b are integers 
A decimal number that does not terminate and does not repeat is called an irrational number.
While the rational numbers can be depicted as a nested diagram as shown, irrational numbers cannot be so depicted. A number cannot be both rational and irrational at the same time.
By virtue of their unending patternless digits, irrational numbers are well suited to code construction.
You learned how to locate irrational numbers on a number line using several methods. The first one used a calculator to evaluate the irrational number. The second method involved using benchmarks to approximate the location of an irrational number. The third method, less efficient, though more accurate than the others, was to use a compass and straightedge to place an irrational number on the number line precisely. You also practised sorting a set of numbers into rational and irrational numbers.
In the next lesson you will learn how to simplify radicals.