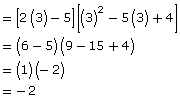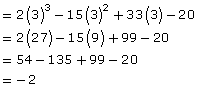Lesson 2: Multiplying Polynomials
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 2: Multiplying Polynomials |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:27 AM |
Module 3: Polynomials
Lesson 2: Multiplying Polynomials
Focus
 © Laurin Rinder/shutterstock
© Laurin Rinder/shutterstock Throughout this unit you have been examining ciphers. For a cipher to be useful, several things must be known by those who are using it:
- the algorithm, or method, used to encipher the plaintext
- the key used with the algorithm to allow the plaintext to be both enciphered and deciphered
- the period of time during which the key is valid
As an analogy you would put a key in a lock to open the door to get into your home. This process (e.g., the use of a key and a lock) is the method or algorithm. Now this method only works if you have the proper key to put in the lock, and your key will be valid only as long as you live in that house. The next owner will have the locks changed so that you cannot enter, even though you may know the method.
Now you may have a new system that uses a code instead of a physical key. This system requires that you pick a security code for your home’s alarm system. It’s very important that you remember the security code and that you follow a few guidelines. It could be a terrible situation if you chose a code that allows intruders to crack the code easily and gain access into your home. For instance, you are advised not to use phone numbers, birthdays, anniversary dates, or other special dates for security codes because these are too easy for other people to find or to guess.
Your new skills in working with polynomials and verification in this lesson may help you in setting codes that are very difficult to guess.
Outcomes
At the end of this lesson, you will be able to
- verify a polynomial product by substituting numbers for the variables
- multiply two polynomials symbolically and combine like terms in the product
- generalize and explain a strategy for multiplication of polynomials
- identify and explain errors in a solution for a polynomial multiplication
Lesson Questions
- How is the distributive property extended to solve multiplication problems as well as other types of problems?
- How can you tell if two polynomials have been multiplied correctly?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 3: Polynomials
Launch
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. Use algebra tiles to multiply the following binomials together. Sketch the answer of the final arrangement of the tiles.
a. (x + 1)(x – 5)
b. (3x – 2)(2x – 3)
2. Use the distributive property to confirm the products in question 1.
a.
b.
3. Collect like terms and simplify the following polynomial expressions.
a. 2x2 + 6x – 5x –15
b. 7 + 8x – x2 – 11x + 3x2 – 10
4. Evaluate the following expressions when x = 2.
a. 4x2 – 8x + 3
b. (2x – 3) (2x – 1)
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Go to “Using the Area Model to Illustrate a Binomial Times a Binomial.” This video will show you how an area model can be used to apply the distributive property in binomial multiplication.
----------------------------------------------------------------
To watch a video to help you recall how to add and subtract monomials, watch the Math Dude video on “Polynomial Operations.”
------------------------------------------------------------------
To review how to evaluate algebraic expressions, go to the Worls of Math online site and watch “Evaluating Expressions.”
-------------------------------------------------------
Materials
For this lesson, you may wish to use the set of algebra tiles that you created from the “Algebra Tiles Template, which is available in the Toolkit.
Alternatively, you could continue to use the “Arranging Algebra Tiles” applet that is also available in the Toolkit.
Module 3: Polynomials
Discover
In the Discover section you will focus on the locations of like terms in a multiplication array. You will also discover a way to verify the product of two polynomials.
 Try This 1 - 5
Try This 1 - 5
Print (or copy by hand) the following questions and complete them in your course folder ( binder).
Use the link below to check your answers to Try This 1 - 5.
Possible TT1-5 (Try This 1 - 5 ) Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 3: Polynomials

Courtesy of Nathan Sawaya, http://brickartist.com.
Nathan Sawaya plays life-size cello made out of Lego pieces.
Explore
Nathan Sawaya is an artist who uses Lego building blocks as his medium. A former lawyer, Nathan is now making his childhood passion a full-time career.
Polynomials, such as binomials and trinomials, can be combined with other polynomials—much like toy building blocks can be combined with others of its kind.
Glossary Terms
Add these terms and their definitions to your Glossary Terms page in your notes. You may also want to add examples that demonstrate how each term is applied.
- verify
--------------------------------------------------
In Lesson 1 of this module you learned to use the area method as well as the distributive property to find the products of binomials. You can apply those same methods to the multiplication of any two polynomials.
Example 1
Multiply (2x – 5)(x2 – 5x + 4) using each of the following two methods:
- area method
- distributive property
Solution: Area Method
Step 1: Set up a multiplication array with (2x – 5) along the left column and (x2 – 5x + 4) along the top row.
|
|
x2 |
–5x |
4 |
|
2x |
|
|
|
|
–5 |
|
|
|
Step 2: Complete the array.
|
x2 |
–5x |
4 |
|
|
2x |
2x3 |
–10x2 |
8x |
|
–5 |
–5x2 |
25x |
–20 |
Step 3: Collect and combine like terms.
 Tip
Tip
Notice that the like terms are found along the diagonals (as highlighted in boldface). As long as you write the terms of each polynomial in descending powers of x, you will always find the like terms along these diagonals.
2x3 – 10x2 – 5x2 + 8x + 25x – 20 = 2x3 – 15x2 + 33x – 20
Solution: Distributive Property
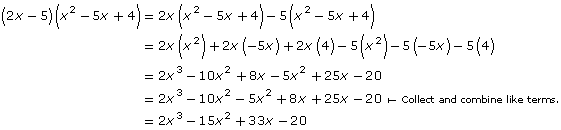
Retrieve your results from TT 1. You substituted a known value (x = 2) into the original multiplication expression. You discovered that the result was the same as when you substituted the same value into the expression representing the final product. The fact that the two results are equal makes sense since the two expressions are equal.
The following example shows how you can verify a product of two polynomials by using a two-column method.
Example 2
Verify the product in Example 1 by substituting x = 3.
Solution
- Create a chart divided into a left-hand column and a right-hand column.
- Substitute x = 3 in both expressions.
- See if the results are equal.
|
(2x - 5)(x2 - 5x + 4) |
2x3 – 15x2+ 33x – 20 |
|
|
|
Since both sides equal to the same value—in this case, –2—you have successfully verified the product expression to be correct when x = 3.
 Self-Check
Self-Check
Take the opportunity to apply the concepts you have learned to these questions. Check your solutions afterwards.
SC 1. Multiply (3x – 5)(5x + 2) using the distributive property, and verify your answer.
SC 2. Multiply (y + 4)(y2 + 2y – 7) using the area method, and verify your answer.
 Try This 6 - 7
Try This 6 - 7
Practice the methods you have learned for multiplying polynomials.
Complete the following in your course folder ( binder).
TEXTBOOK: Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. Complete “Exercises” questions 8 and 10 on page 186.
TT 7. a. Choose at least two of the questions in TT 6 to verify. How do you select a value of x to use in verifying?
b. Are there values that are better suited for verifying than others?
Use the link below to check your answers to Try This 6 - 7
Possible TT6-7 (Try This 6 - 7) Solutions
-----------------------------------------------------------------
What happens if you verify a solution and you do not get results that are equal? In those cases, you may have committed an error either in your original multiplication or in the verification. In the remainder of this lesson, you will identify and explain common errors in solutions for polynomial multiplication.
 Self-Check
Self-Check
For questions SC 3 and SC 4, you will be required to analyze a polynomial multiplication for errors. Try to identify the error and also explain how the expansion is carried out correctly. You may also wish to try to expand it on your own; then compare your solution with the given one.
SC 3. Michael expanded the following expression.
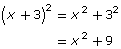
SC 4. Salma expanded the following expression.
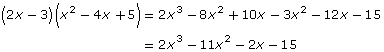
 Try This 8
Try This 8
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 8. a. Complete “Exercises” question 13 on page 167.
b. Complete “Exercises” questions 11 and 14 on page 186.
Use the link below to check your answers to Try This 8.
Possible TT8 (Try This 8) Solutions
 Watch and Listen
Watch and Listen
Go the Khan Academy page linked below. You will find five questions to practice. If you have problems, there is a link to a video on the lower right corner.
Harder Multiplication questions
Example 3: Expand and simplify the following expression.
2( 3x - 1)( x + 2) - (x - 3) ( x + 4)
Solution 3:
Step 1: Start with doing FOIL on the first set of brackets and the last set of brackets.
2( 3x2 + 6x - 1x - 2) - ( x2 + 4x - 3x - 12)
Step 2: Collect the middle terms
2( 3x2 + 5x - 2) - ( x2 + x - 12)
Step 3: Multiply the 2 through the first bracket and the -1 through the second bracket. ** Note the subtraction sign is written as -1.
2( 3x2 + 5x - 2) -1 ( x2 + x - 12)
= 6x2 + 10x - 4 - x2 - x + 12 ** note the sign change in the last terms
Step 3: Collect like terms and finish
= 5x2 + 9x + 8
 Try This 9
Try This 9
Complete the following questions in your course folder ( binder).
Do all of the work and then use the link below to check your work.
a. -2( x - 5) (2x - 4) - ( 2x - 1)2
b. 3( 2a - 4b) ( 3a + 2b) + 5(4a- 1) ( 4a + 1)
Module 3: Polynomials
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

© Pedro Angeles/iStockphoto
If you have ever watched a movie about espionage, you may have viewed a scene where two spies meet at a prearranged place to share classified information. Since the spies have never met before, they use secret passwords or phrases to ensure that they are sharing the information with the right person and not an enemy. This type of security measure is not limited to the realm of espionage; it is also evident in your day-to-day world.
A personal identification number, or a PIN, is often issued to you when you open a bank account or apply for a credit card. The PIN serves as a secret key to allow you to access secure information. In addition to this level of security, you are often also asked to provide an answer to a question that only you would know.
Examples of such questions might include the following:
- What is your mother’s maiden name?
- What is an important date for you?
- What was your favourite book as a child?
- What was the name of your first pet?
In the event that you lose your credit card or forget your PIN, you can still access information through a customer service agent. An agent will verify your address and birth date. This information, however, could be obtained by an unauthorized person. So in order to ensure that you are who you say you are, the agent will ask you to provide the answer to a predetermined question.
You can also use math concepts from this lesson to develop a similar security measure. Study the following example.
In this system, one person communicates a key word to the second person. The second person then communicates a number to the first person. The number that is communicated is based on an algorithm involving the letters of the key word.
In this algorithm, it will be important to know the position of each of the letters in the alphabet. Here is a table that can be used to identify letter positions.

Step 1: Assume the password is CARS. Write each letter in a table and its letter position according to the table above.
|
Letter |
Position |
|
C |
3 |
|
A |
1 |
|
R |
18 |
|
S |
19 |
Step 2: The first letter is a reference letter for the next two letters. In your box, subtract the position of the first letter from the positions of each of the second and third letters.
|
Letter |
Position |
|
|
C |
3 |
|
|
A |
1 |
1 – 3 = –2 |
|
R |
18 |
18 – 3 = 15 |
|
S |
19 |
|
Step 3: Place an x in front of each of these numbers to create two binomials.
|
Letter |
Position |
|
|
|
C |
3 |
|
|
|
A |
1 |
1 – 3 = –2 |
x – 2 |
|
R |
18 |
18 – 3 = 15 |
x + 15 |
|
S |
19 |
|
|
Step 4: Multiply the binomials together.
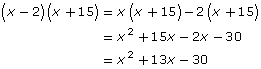
Step 5: Substitute the position of the last letter into the result from step 4.
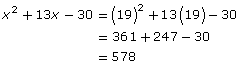
In this system, one person would communicate the key word to the other individual. The other individual would then perform the calculations in order to be able to respond with the correct number.
At this time, go to the Unit 2 Project and complete the Module 3: Lesson 2 portion of the project.
 Going Beyond
Going Beyond
In the Going Beyond section of Lesson 4 in Module 2, you investigated pencil-and-paper techniques for approximating square roots. One such method is by using a Taylor polynomial. Named for mathematician Brook Taylor, the Taylor polynomial can be used to approximate the square roots of numbers between 0 and 2.
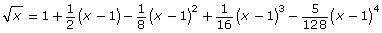
- Evaluate the formula when x = 0.8.
- What irrational number have you approximated?
- Use your calculator to evaluate the irrational number. How does the calculator’s answer compare with what you obtained in question 1?
Use the Internet to further explore how other types of polynomials are used in math or real-world applications. You could also research what other mathematical contributions were made by Brook Taylor.
Module 3: Polynomials
Lesson 2 Summary
In Lesson 2 you investigated the following questions:
- How is the distributive property extended to solve multiplication problems as well as other types of problems?
- How can you tell if two polynomials have been multiplied correctly?
In this lesson you learned to use the distributive property to multiply binomials. The distributive property is used to “pair” each term of one polynomial with another polynomial.
You learned that one way to keep track of which terms have been paired with others is by using a multiplication array.
You applied the strategies you learned in the previous lesson to multiply polynomials. These strategies included the use of a multiplication array, or area method, and the distributive property. While these strategies have different names, they are both based on the concept that each term of one polynomial is multiplied to each term of the second polynomial.
As the polynomials used in these calculations get bigger, so too does the risk of committing an error increase. Therefore, it is necessary to have a way of verifying that the solution is correct. You learned to verify a product by substituting a numerical value for x into both the original expression as well as the obtained product. If both resulting values were equal, then the product was verified to be correct.
In the Reflect and Connect section you explored other types of problems that can be solved by using a multiplication array and applying the concept of the distributive property. You realized the benefit of the array as a visualization tool that could help you to keep track of information. You have also learned that the distributive property is applicable to an assortment of mathematical problems, not only in the area of polynomials. You will continue to see these sorts of problems in future math courses.
Factoring is the next topic you will investigate. You can recover the factors of a polynomial by applying an appropriate factoring strategy. In the next lesson you will learn how to factor polynomials using the greatest common factor method. You will also begin exploring ways of factoring trinomials.