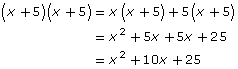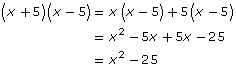Lesson 5: Factoring Special Polynomials
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 5: Factoring Special Polynomials |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:23 AM |
Module 3: Polynomials
Lesson 5: Factoring Special Polynomials
Focus

François Viète was an amateur mathematician.
François Viète was a French amateur mathematician and astronomer who introduced the first systematic algebraic notation in his book In artem analyticam isagoge.
He was also involved in deciphering codes. While working for King Henry III in 1590, François Viète discovered the key to a Spanish cipher of 500 characters. Viète’s code-cracking skills allowed him to read the secret correspondence of France’s enemies, which, of course, gave the French a huge advantage over the Spanish. You will also add to your code-cracking and code-creating abilities by using the methods learned in this lesson to add to the complexity of your own secret code for your unit project.
In previous lessons you learned how to factor polynomials using such methods as common factors, product-sum, decomposition, and inspection. In Lesson5 you will explore a method used to factor a difference of squares.
Outcomes
At the end of this lesson, you will be able to
- factor a polynomial that is a difference of squares, and explain why it is a special case of trinomial factoring where b = 0
- generalize and explain strategies used to factor a trinomial
Lesson Questions
-
How are perfect squares involved in the factoring of polynomials?
-
How do you select appropriate strategies for factoring polynomials?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 3: Polynomials
Launch
Are You Ready?
Print (or copy by hand) and complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Lesson 5: Are you ready questions.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
1. Review the basics of extracting a square root from a monomial by watching “Square Root of a perfect square monomial"
2. To watch a video to see how the acronym FOIL can help you apply the distributive property when you are multiplying binomials, go to the video "Math Dude - Multiplying Polynomials.”
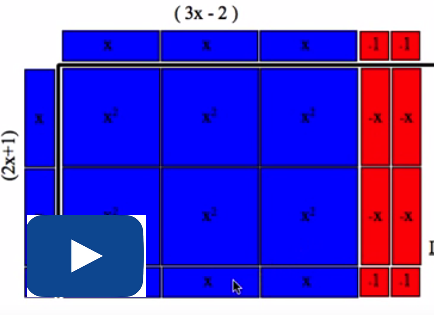
3. Now watch “Mathcast 009 Using the Area Model to Illustrate Common Factoring of a Monomial and Binomial” which reviews how you can use algebra tiles to model factoring by greatest common factor.
4. Watch “Mathcast 010 Using the Area Model to Factor Trinomials” that demonstrates how algebra tiles are used to model both binomial factors and trinomial products.
5. Finally, watch “Mathcast 012 Factoring—Decomposition Examples” . This video reviews the steps of decomposition and shows how these steps are applied to several examples.
Materials
-
graph paper
- scissors
Discover
![]() Math Lab: Investigating a Difference of Squares
Math Lab: Investigating a Difference of Squares 
Print (or copy by hand) and Complete Math Lab: Difference of Squares
Math Lab: Difference of Squares
Use the link provided to check your work. *** DO the work before checking - this will lead to much better understanding**
Module 3: Polynomials
Explore
Glossary Terms
Add these terms to your "Glossary Terms' in your notes:
-
conjugate binomials
-
difference of squares
-
perfect square trinomial

© Dimanchik/shutterstock
--------------------------------------------------------------------
Factoring a Difference of Squares
A special case of a trinomial is known as a difference of squares. You will recognize a polynomial as a difference of squares when you observe that the polynomial
-
is a binomial
-
has a first term that is a perfect square
-
has a second term that is a perfect square
-
shows the subtraction of one term from another
As an example, x2 – 4 is considered a difference of squares since both x2 and 4 are perfect squares and one is being subtracted from the other. Although x2 – 4 is expressed as a binomial, it can be viewed as a trinomial whose x-term has a coefficient of zero. In other words,
x2 – 4 = x2 + 0x – 4
When viewed this way, a difference of squares can be factored by using trinomial factoring methods. In this case, you can use the product-sum method.
Example 1
Factor x2 – 4.
Solution
Think about the difference of squares as the trinomial x2 + 0x – 4.
Step 1: Find two numbers whose product equals –4 and whose sum equals 0.
|
First Number |
Second Number |
Product |
Sum |
|
1 |
–4 |
–4 |
–3 |
|
2 |
–2 |
–4 |
0 |
Choose the combination that gives the correct sum. (See the numbers shown in the second row of the chart.)
Step 2: Express the polynomial as a product of its factors.
x2 – 4 = (x + 2)(x – 2)
Do you notice that the two factors are almost identical except for the sign of the constant? These factors are known as conjugate binomials.
 Tip
Tip
Conjugate Binomials: Binomials with the same terms but different sign between the terms.
ie: ( x + 2) and ( x - 2) are conjugate binomials
( 3x - 2) and ( 3x + 2) are conjugate binomials
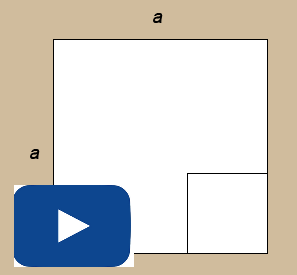
There is another method of factoring a difference of squares. In the Discover section you used graph paper to visualize a difference of squares by removing a square with smaller dimensions from one with larger dimensions.
Retrieve and review your Math Lab results. Compare the last three columns of your completed table to the one below.
|
Dimensions of Original Square |
Dimensions of Removed Square |
Rectangle Length |
Rectangle Width |
Rectangle Area |
|
10 × 10 |
6 × 6 |
10 + 6 |
10 – 6 |
(10 + 6)(10 – 6) |
|
8 × 8 |
3 × 3 |
8 + 3 |
8 – 3 |
(8 + 3)(8 – 3) |
|
7 × 7 |
4 × 4 |
7 + 4 |
7 – 4 |
(7 + 4)(7 – 4) |
|
5 × 5 |
2 × 2 |
5 + 2 |
5 – 2 |
(5 + 2)(5 – 2) |
Can you see how the area of the rectangle can be determined by knowing only the dimensions of the original square and the removed square?
 Watch and Listen
Watch and Listen
Watch the video titled “Difference of Squares” to see how this pattern can be generalized for any square.
Example 2
Factor 9x2 – 4y2 completely and check by multiplying.
Solution
Step 1: Determine the square roots of 9x2 and 4y2.
![]()
![]()
Step 2: Write one factor as the sum of the square roots. Write the other factors as the difference of the square roots.
9x2 – 4y2 = (3x + 2y)(3x – 2y)
Step 3: Check by multiplying.
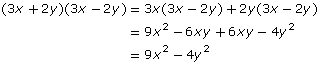
The original difference of squares is recovered, so the factors are correct.
Example 3
Factor 2m4 – 162 completely and check by multiplying.
Solution
Step 1: Check for common factors.
![]()
The greatest common factor is 2.
Therefore, 2m4 – 162 = 2(m4 – 81).
Step 2: See if you can continue to factor the binomial.
You can continue to factor m4 – 81 as a difference of squares.
Determine the square roots of each term in the difference of squares.
![]()
![]()
Therefore, 2(m4 – 81) = 2(m2 + 9)(m2 – 9).
Step 3: See if you can continue to factor the binomials.
You can continue to factor the binomial m2 – 9 as a difference of squares.
m2 = m × m
9 = 3 × 3
So, 2(m2 + 9)(m2 – 9) = 2(m2 + 9)(m + 3)(m – 3).
 Tip
Tip
Remember that you can only factor a difference of squares, not a sum of squares.
So, m2 – 9 = (m – 3)(m + 3), but m2 + 9 cannot be factored.
Step 4: Check by multiplying.
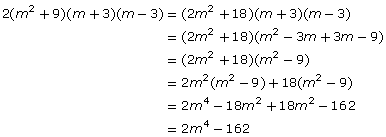
The original difference of squares is recovered, so the factors are correct.
 Watch and Listen
Watch and Listen
You have just learned two ways to approach the factoring of a difference of squares. If you feel that you would benefit from another explanation, go to the YouTube website “Mathcast 014 Using Algebraic Patterning to Factor a Difference of Squares” video.
 Read
Read
In your textbook, there are some additional examples of factoring a difference of squares using the ideas developed in this lesson. As you read, check that the polynomials meet the conditions for factoring as a difference of squares.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Factoring a Difference of Squares” on page 193. How do you factor a difference of squares if the coefficients of the binomial are not perfect squares? How do you deal with terms with two variables?
 Self-Check
Self-Check
SC 1. For each of the following questions, decide if the expression can be factored as a difference of squares. If so, factor the expression completely. If not, explain why it cannot be factored.
- x2 + 4
- –9x2 + 36y2
- –x2 – 49
- 81x2 – 144y2
 Try This 1
Try This 1
Apply the method of factoring a difference of squares to these questions from your textbook. Remember that certain conditions have to be met before this technique can be used to factor a polynomial. You may want to review these conditions before you attempt these questions.
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” questions 6.b), 6.d), 10.a), 10.c), 10.e), 10.g), and 21 on pages 194 and 195.
Use the link below to check your answers to Try This 1.
Possible TT1 (Try This 1) Solutions
Factoring Perfect Square Trinomials

Another type of special polynomial is the perfect square trinomial. A perfect square trinomial is the result of squaring a binomial.
Try the following exercise to see if you can uncover a pattern for factoring perfect square trinomials.
 Try This 2 - 8
Try This 2 - 8
Print (or copy by hand) and complete the following in your binder.
Use the link below to check your answers to Try This 2 - 8.
Here is an example of how you can factor a perfect square trinomial.
Example 4
Factor 9x2 + 12x + 4.
Solution
Step 1: Before you can apply a special strategy, you need to confirm that the trinomial is in fact a perfect square trinomial.
Are the first and last terms perfect squares?
Check:
9x2 = 3x × 3x
4 = 2 × 2
Both terms are perfect squares.
Is the middle term equal to twice the product of the square roots of the first and last terms?
Check:
2 × 3x × 2 = 12x
Yes, the middle term is twice the product of the square roots of the first and last terms.
Step 2: Write the trinomial as the product of two identical binomials whose terms are equal to the sum of the square roots of the first and last terms of the trinomial.
9x2 + 12x + 4 = (3x + 2)(3x + 2)
OR
9x2 + 12x + 4 = (3x + 2)2
What if you fail to recognize that a trinomial is a perfect square trinomial? Can a perfect square trinomial still be factored by the other methods that you have learned?
 Try This 9
Try This 9
Complete the following in your binder.
TT9: a. Factor 9x2 + 12x + 4 using at least two of the other trinomial factoring methods, such as algebra tiles, product-sum, decomposition, or inspection.
b. What conclusion do your results suggest? Do the results of factoring by other methods lead to the same answer?
Use the link below to check your answers to Try This 9.
Possible TT9 (Try This 9) Solutions
 Read
Read
Read the following example to see how a perfect square trinomial can be factored by other methods. As you read, think about how you can modify your strategy of factoring perfect square trinomials so you can check the middle term at the end.
|
Foundations and Pre-calculus Mathematics 10 (Pearson) Read “Example 1: Factoring a Perfect Square Trinomial” on page 190. |
 Try This 10
Try This 10
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 10. Complete “Exercises” questions 4.c), 4.d), 8.a), 8.c), 8.f), 13.b), and 18 on pages 194 and 195.
Use the link below to check your answers to Try This 10.
Possible TT10 (Try This 10) Solutions
 Self-Check
Self-Check
As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur. Some of these errors are due to inattention to details. Other types of errors reveal a misconception of the recently learned math principles.
The following Self-Check questions show how a student may factor a polynomial using the methods learned in this lesson.
SC 2. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.
1. Factor x4 – 16 completely.
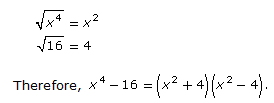
Since both x2 and 4 are perfect squares, this expression can be factored further.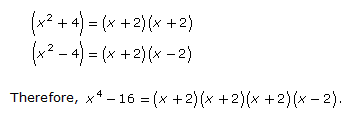
2. Factor 9x2 + 30x + 16.
Since both 9x2 and 16 are perfect squares, 9x2 + 30x + 16 is a perfect square trinomial.
 Try This 11
Try This 11
Complete the following in your course folder ( binder). File them in your binder for future reference.
Practise troubleshooting factoring solutions. Be sure to identify the error and also correct it.
TT 11. Identify the error in each of these solutions. Then correct the error and complete the solution.
a. Factor 4x2 – 4x + 1. Since both 4x2 and 1 are perfect squares, 4x2 – 4x + 1 is a perfect square trinomial.
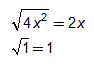
Therefore, the factored form is (2x + 1)2.
b. Factor (x2 – 5)2 – 16 completely. This is a difference of squares.
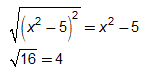
Therefore,
(x2 – 5)2 – 16 = ( x2 - 5 - 4)( x2 - 5 + 4)
= ( x2 - 9) ( x2 - 1)
Since both x2 and 9 are perfect squares:
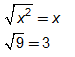
(x2 – 5)2 – 16 = ( x2 - 5 - 4)( x2 - 5 + 4)
= ( x2 - 9) ( x2 - 1)
= ( x - 3) ( x + 3) ( x2 - 1)
Use the link below to check your answers to Try This 11.
Possible TT11 (Try This 11) Solutions
 Key Ideas
Key Ideas
Part A
Return to your Factoring Strategies document. Update the document with the methods used in this lesson to factor differences of squares and perfect square trinomials. You should now have information in your chart about multiple types of factoring, including the following:
-
common factors
-
trinomial factoring
-
grouping
-
differences of squares
-
perfect square trinomials
With a partner ( if possible), compare the information that the two of you have included in your respective charts. Keep in mind that your chart is personal to you, so you may not have the same worked examples or tips about using a particular strategy. You may, however, notice some information in your partner’s chart that may be of benefit to you.
Reflect on these questions as you meet with your partner:
-
Am I missing any strategies that have been included on my partner’s chart but not mine? Should I include this information?
-
Are there any tips that I can pick up from my partner about a particular strategy?
-
Do I see any misconceptions in my partner’s chart? Does my partner’s chart reveal any misconceptions on my part?
-
Are my partner’s worked examples done correctly? Does my partner notice any errors in my examples?
Make any revisions you feel would improve your chart as a study tool and review document. You may wish to repeat this exercise with another partner.
Part B
© Sideways Design/shutterstock
Another way you can represent the information you have added to the “Factoring Strategies” document is by using a flow chart. A flow chart can help you to visualize the steps required to factor a polynomial. The ability to visualize is especially helpful in cases where multiple steps are required before a polynomial is completely factored.
Using the information in your Factoring Strategies document, create a flow chart that helps you to decide when to use a certain factoring strategy.
To get an idea for how you can design this piece, go to the Internet and enter the keywords “Mathcast 015 Strategies for Solving Mixed Factoring Problems” in a search engine. This search should lead you to a video posted on YouTube. As you watch, try to identify what you need to know about a polynomial before you can select a factoring strategy.
You may also want to perform an Internet search using the keywords “factoring flow chart” or “factoring polynomials” and other related keywords to help guide you when you create your flow chart.
Put a copy of your flow chart in your binder.
You may use it along with your Factoring Strategies document to review key principles covered in this module.
Module 3: Polynomials
Connect
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activites block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**
Recall the Discover activity in this lesson where a smaller square was cut and then removed from a larger square. This could be the basis for a cipher.
For example, if you wanted to encrypt the message “MATHEMATICS IS FUN,” you can do so with a 4 × 4 word square like the ones you learned about in Lesson1. A variation on that cipher is to encrypt the message in a larger 5 × 5 square. The following is a description of how that might be done.
Encrypt the phrase MATHEMATICS IS FUN using a variation of the word square cipher.
Step 1: Construct a 5 × 5 grid.
Step 2: Since the phrase has 16 letters and the square has 25 cells, you will not need to use all of the cells for your message. The nine squares in the lower-right corner will not be used for letters of the message. This area has been shaded to remind you of this.

Step 3: Place the letters of your message according to the order noted in the following diagram.
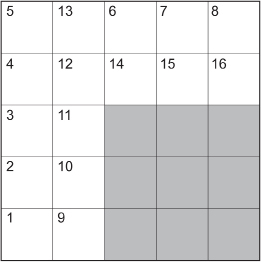
In this case:

Note: The reasoning behind the letter placement is found in the Math Lab. You would get the following if you removed the shaded square, vertically cut the remaining L-shape into two rectangles, and reassembled the two rectangles into a longer rectangle:

Step 4: Fill the shaded region with random letters.

Step 5: Write the letters of the message in order from left to right. You have a choice of writing the letters in blocks with spaces in between or with no spaces in between.
ESMATHIF U NTSHEN AC ARDM INTS.
Your message is now encrypted.
Step 6: Construct a key. You will need a key to help the intended recipient of your code to decipher the message. He or she will need to know two things:
-
dimensions of the larger square
-
dimensions of the smaller (shaded) square
The following algorithm shows a simple way to create a key that provides both important pieces of information:
|
Step |
Action |
Example |
| 1 |
Set up the dimensions of the larger square as a binomial square or a product of conjugates. Then expand. |
OR
|
| 2 |
Multiply each term of the polynomial by the dimension corresponding to the side length of the smaller square. |
|
Now go to the Unit 2 Project and complete the Module 3: Lesson 5 portion of the project.
 Going Beyond
Going Beyond

© Yuganov Konstantin/shutterstock
Have you read some of the e-mail math tricks that get sent around? The e-mails are about how a “magic formula” can be used to guess your age or your secret number. All of these tricks are based on algebra—don’t let them fool you!
You have learned that a2 – b2 = (a + b)(a – b).
But perhaps you haven’t thought about how to use this to do fast mental calculations. See if you can guess how this trick can help you do the following in your head:
43 × 37
78 × 82
36 × 24
Do you see the pattern with these numbers?
Let’s do the first one.
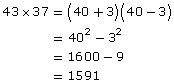
Practice these and you’ll be able to impress your friends or your family members! If you think creatively about everything that you learn in mathematics and look for patterns, you will find some surprising applications.
Module 3: Polynomials
Lesson5 Summary
In this lesson you investigated the following questions:
-
How are perfect squares involved in the factoring of polynomials?
-
How do you select appropriate strategies for factoring polynomials?
In this lesson you discovered patterns that helped you to develop strategies for factoring special polynomials. What is common to each of these polynomials is that they both involve perfect squares. In the case of a difference of squares, you learned that
a2 – b2 = (a + b)(a – b)
The pattern you discovered here is that a difference of squares can be expressed as the product of the sum of the square roots and the difference of the square roots of each term in the original binomial. You also learned that this pattern is only valid in cases where the polynomial to be factored
-
is a binomial
-
has a first term that is a perfect square
-
has a second term that is a perfect square
In this lesson you also discovered patterns relating to perfect square trinomials. These trinomials are identified by the presence of two perfect squares: the x2-term and the constant. You learned that these trinomials can be factored by ordinary trinomial factoring strategies. If you can, however, identify that both the x2-term and constant are perfect squares, you can factor it as a perfect square trinomial.
You have now added many factoring strategies to your repertoire. To decide which strategy or combination of strategies to use, you must be aware of the conditions under which a strategy can be used.
Throughout the last three lessons of this module, you have learned to select strategies based on the nature of the polynomial. In all cases, you should always check each term to see if there are common factors that can be factored first. If further factoring is warranted, then you will have the added benefit of working with smaller coefficients.
Lesson 5 is the last lesson of Module 3. Remember to complete the Unit 2 Project.
You have now completed Module 3. In this module you have learned how to multiply and factor polynomials. In subsequent modules, you will continue to use factoring to achieve other objectives such as simplifying expressions and solving equations.