Lesson 4: Slope
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Slope |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:27 AM |
Module 4: General Relations
Lesson 4: Slope
Focus

© sn4ke/shutterstock
Mountain biking was first included in the Summer Olympics at the 1996 Games in Atlanta, Georgia. There are three other Olympic cycling disciplines: road cycling, track cycling, and BMX, which is short for bicycle motocross. All of the cycling disciplines include both men’s and women’s events.
What are some of the requirements for an Olympic mountain-bike course? The course needs to test the physical endurance and bike-handling skills of riders as they manoeuvre around trees, branches, rocks, and streams. It should include a variety of terrain—forest roads and trails, earth or gravel paths, and significant amounts of climbing and descending. Typically, mountain-biking courses are designed so top competitors will finish them in about two hours.
Since 1996, Olympic mountain-bike courses have varied in length, and riders must complete a specified number of laps. The 2000 Summer Olympics in Sydney, Australia, had a 7-km mountain course that featured steep drops, sharp turns, and paths as narrow as 50 cm. For the 2004 Summer Olympics in Athens, Greece, the 6.1-km mountain-biking course was built in the pine and oak forests of Mount Parnitha. At the 2008 games in Beijing, China, the Laoshan mountain-bike course was shortened to 4.6 km; it had a hard-pack single track covering a series of small climbs through heavy brush and wood and it included berms (banked curves), drops, and rocks, as well as challenging climbing and descent sections.
Designers of mountain-biking trails need to have strong math skills. Because these trails need to have more gradual grades than hiking trails do, a well-designed bike trail will generally follow a contour line across the hill. If the course is built on a steep mountain, there will be several switchbacks. The trail will also slope across the hill at a slight downhill angle; this will encourage water to run off the side of the trail and downhill.
In this lesson you will explore slope. You will investigate what the direction of the slope means and how you can calculate the slope of a line.
Outcomes
At the end of this lesson, you will be able to
-
determine the slope of a line segment by measuring or calculating the rise and run
-
classify lines in a given set as having positive or negative slopes
-
explain the meaning of the slope of a horizontal or vertical line
-
explain why the slope of a line can be determined by using any two points on that line
Lesson Questions
In this lesson you will investigate the following questions:
-
How can slope be used to describe the properties of objects?
-
Why is it possible to use any two points to determine the slope of a line?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 4: General Relations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Print (or copy by hand) and Complete.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
In earlier lessons of this module, you mainly worked with the first quadrant of the coordinate plane. In this lesson you will be working with all four quadrants.
Complete the following game to see if you are ready.
The “Maze Game” activity allows you to practise point-plotting skills by moving a robot through a mine field to a target location.Go to “Quadrant” at the Mathematics Glossary website to review the definition of a quadrant in the coordinate plane. You will also be able to see how the quadrants are named.
 Read
Read
Review the definition of the tangent ratio by studying an example in your textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read the bottom half of page 71 and the top of 72. Then work through “Example 1: Determining the Tangent Ratios for Angles.”
Then go to “Formula” at the Mathematics Glossary website to review some familiar formulas. You will also be able to see how formulas can be rearranged to isolate specific variables.
Materials
-
tape measure or ruler
-
staircase to measure
Module 4: General Relations
Discover

© Felix Mizioznikov/shutterstock
Stairs are made up of treads (the part you step on), risers (the part your toe bumps), and stringers (the structure that holds the treads and risers up). Sometimes, a tread has a nosing (the edge part of the tread that protrudes from the riser beneath).
 Math Lab: Slope of a Staircase
Math Lab: Slope of a Staircase
Find a staircase in your school or your home that you can measure.
Go Math Lab: Slope of a Staircase, print it (or copy by hand) and complete it.
Math Lab: Slope of a Staircase
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder( course folder) to refer to later.
Module 4: General Relations
Explore
In a cold northern climate where the snowfall is heavy, it’s best to have a roof with a steep pitch so that the roof will shed the snow and rain as thoroughly as possible. In a warm southern climate where there is no snow and where the rain fall is not large, a flat roof may be safely used and will be more economical to construct.

© Mark Stout Photography/shutterstock

© Bruce C. Murray/shutterstock
In this lesson you will explore slope. Slope is used to describe the steepness of any feature such as a hill, stream, road, staircase, ramp, or roof.
Glossary Terms
Add the following terms to your "Glossary terms" section in your notes. You may also want to add examples that demonstrate how each term is applied.
-
rise
-
run
-
slope
In mathematics, SLOPE is the ratio of the vertical change to horizontal change or rise over run.
![]()
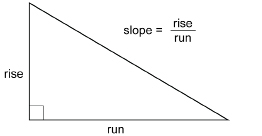
The vertical change is called the rise. The horizontal change is called the run.
 Watch and Listen
Watch and Listen
Watch the short video on “Slope as Rise Over Run.”
 Try This
Try This

© Shchipkova Elena/shutterstock
Many buildings have ramps for people in wheelchairs. In TT 1, you will consider two ramps with different dimensions.
Read the following example to see how you can use the rise/run ratio to calculate the slope of each ramp in the TT 1. Compare this result with your prediction in the previous Try This activity.
Example 1
Many buildings have ramps for people in wheelchairs. The illustration below shows two ramps with different dimensions. Predict which ramp is steeper. Use the rise/run ratio to determine which ramp is steeper. Support your reasoning without using a calculator. Do your work in your course folder ( binder).
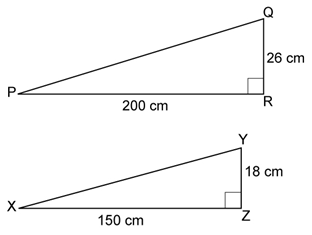
Step 1: Determine the slope of each ramp.
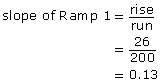 |
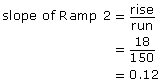 |
The slope of Ramp 1 is 0.13. The slope of Ramp 2 is 0.12.
Step 2: Compare the slopes.
0.13 > 0.12
Ramp 1 has the steeper slope.
 Try This 2 - 7
Try This 2 - 7
You will analyze a number of lines in a coordinate plane and compare these lines with respect to their slope.
Print and complete the following in your course folder ( binder).
Try This 2 - 7
Use the link below to check your answers to Try This 2 - 7.
Possible TT2 - 7 (Try This 2 - 7) Solutions
 Watch and Listen
Watch and Listen
Watch the “Investigating Slope” video to see how you can use points to determine the rise and run of a line. After viewing the video, you will do another Try This Activity. Username LA53, password 4487.
 Try This 8 - 10
Try This 8 - 10
As you worked through the examples of calculating the slopes of lines, did you see another possible way to find the rise and run?
Complete the following in your course folder ( binder).
TT 8. What if you wanted to start at a different point on the graph? Would it make a difference in the value of the slope? Why or why not?
TT 9. What if you started at a point that was higher up on the graph and counted down to the next point? Would that make a difference in the value of the slope? Why or why not?
TT 10. Suppose the slope is an integer. How do you identify the rise and the run?
Use the link below to check your answers to Try This 8 - 10.
Possible TT8 - 10 (Try This 8 - 10) Solutions
 Self-Check
Self-Check
Now that you have seen a demonstration of how to calculate the slope of a line using two points on the line, you can apply what you have learned to the following exercise.
SC 1. Calculate the slope of the red and blue lines.
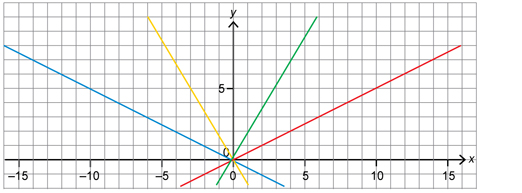
Slope of a Line Segment
 Try This 11 - 14
Try This 11 - 14
Use the Interactive Slope Applet to help answer the questions. You can drag the slider from -10 to positive 10 and watch what happens to the slope.
Keep your eye on the slope so you can see how it changes as you change the line.
As you explore with this applet, determine the following.
Complete these in your course folder ( binder).
TT 11. How are all line segments with positive slope similar?
TT 12. How are all line segments with negative slopes similar?
TT 13. a. What is the slope of a horizontal line segment?
b. Does the slope change as its length increases?
TT 14. a. What is the slope of a vertical line segment?
b. Does the slope change if the line segment is located in another part of the graph?
Use the link below to check your answers to Try This 11 - 14.
 Read
Read
Confirm your ideas about slope by reading your textbook. As you read, look for the reason why positive slopes are positive and negative slopes are negative.
|
Foundations and Pre-calculus Mathematics 10 (Pearson) Go to page 335, and read the bottom half of the page. Start reading where the vertical blue line shows along the page. |
How can you explain the values of the slopes of horizontal and vertical line segments?
Example 2
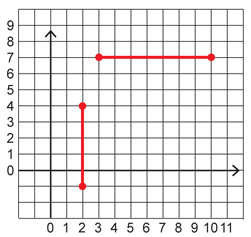
Using the diagram, determine the slope of the following:
- the horizontal line segment
- the vertical line segment
Solution
- In the graph of the horizontal line segment, the rise is zero units and the run is 6 units.
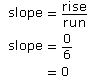
All horizontal line segments are flat and have a rise of zero. Since zero divided by any other number (besides zero) is zero, the slope of any horizontal line segment is zero. - In the graph of the vertical line segment, the rise is 5 units and the run is zero.

All vertical line segments have a run of zero. Since any number divided by zero is undefined, the slope of any vertical line segment is undefined.
 Print
Print
Print the following page for a summary of lines and their slopes.
Here is a fun way to remember slope - can you figure out what everything means on Mr. Slope guy?
Retrieve your Math Lab results. In the Discover section of this lesson, you investigated the steepness of a staircase. Since you were evaluating the rise divided by the run of a step, you now know that you were actually evaluating the step’s slope.
You may have noticed that the slope of a single step is equal to the slope of the entire staircase. Also, you may have discovered that the slope of one step is equal to the slope of any number of consecutive steps. This makes sense since a staircase is much safer if the steps are consistently steep.
Have you ever walked on stairs with steps that were not of consistent steepness? Or perhaps you have stepped onto or off of an escalator? What are the hazards of steps of varying slopes?
Just as the slope of a staircase can be determined by using any two steps along the staircase, the slope of a line or any segment of a line can be determined by knowing the location of any two points along the line or segment.
 Watch and Listen
Watch and Listen
There is a formula that you can use to determine the slope of any line, as long as you know the coordinates of two points on the line. Watch the “Slope of a Line” video to find out how to derive this formula. **Scroll down to find the video**
For this video, you will only need to watch certain segments. Watch from the beginning to the 1:05 minute mark. Then watch the section from 1:45 minutes to 4:05 minutes. As you watch these video segments, try to determine how the points are named.
When you know two points with coordinates (x1, y1) and (x2, y2), you can determine its slope, m, by using the following formula:
![]()
 Read
Read
Go to your textbook to see another example of how the slope formula is used. As you work through the example, think of those instances in which it may be more practical to use the formula than to use the rise over run method.
Foundations and Pre-calculus Mathematics 10 (Pearson)Read “Example 3: Determining Slope Given Two Points on a Line” on page 337. |
 Self-Check
Self-Check
SC 2. Use the slope formula to evaluate the slope of the line that passes through each pair of points.
- A(1, 3) and B(4, 9)
- C(−5, 12) and D(11, 6)
 Try This 15
Try This 15
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 15. Complete “Exercises” questions 4, 5, 6, 13, and 16 on pages 339 to 341. Note: For question 13, use the slope formula.
Use the link below to check your answers to Try This 15.
Possible TT15 (Try This 15) Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 4: General Relations
Connect
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**

© Vladimir Nikulin/shutterstock
There are numerous sporting events that rely on slope. Rock climbing and bobsled racing are two of those sporting events.
In the Lesson 4 component of the Unit 3 Project, you will be required to choose a sporting event that includes slope in some way.
First, you will be required to provide a graph and a description of when you would have each of the following situations:
-
a positive slope
-
a negative slope
-
a slope of 0
-
an undefined slope
For each of the four situations, you will provide two points on your graph and show the rise/run slope calculation.
Next, you will be required to perform an Internet search to find out about slope as an aspect of design. Report on an area of interest where the construction of a particular slope is critical to the purpose of an event or activity. For example, you may want to find out about how the design of a ski-jumping hill facilitates safe landings. You may venture outside the realm of sports and consider the design of such things as the slope of the landing strip for a space shuttle.
The following is a sample project.
Event: Mountain Biking

© jean schweitzer/shutterstock
- Provide a graph and a description of when you would have each of the following.
- a positive slope
As the bike rider is climbing the hill (or riding the chairlift), this would represent a positive slope. The graph shows the bike rider starting at 100 ft above sea level and reaching a height of 700 ft after 24 min.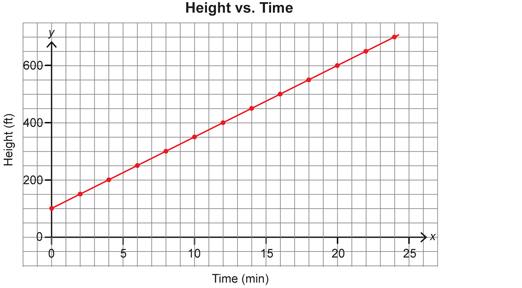
Two points on this graph include (0, 100) and (10, 350).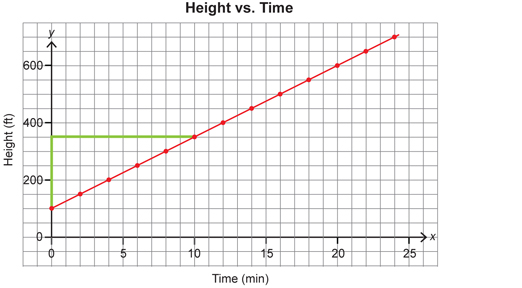

- a negative slope
The mountain biker is now at the top of the hill, at 700 ft, and the trail takes the rider down the other side of the hill, with a steeper slope. The rider is descending the hill and the graph slopes from left to right, so this shows a negative slope.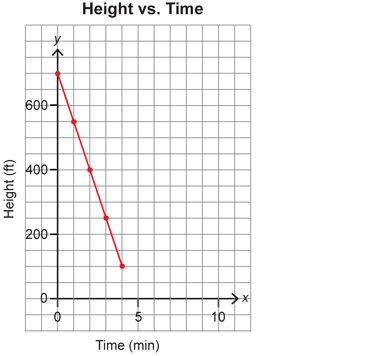
Two points on this graph include (0, 700) and (2, 400).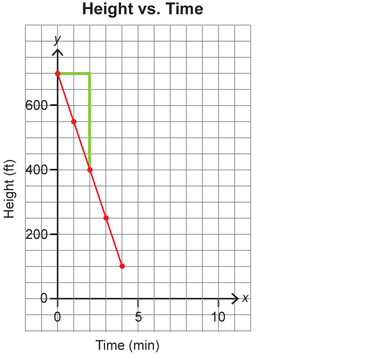
- a slope of 0
When the mountain biker reaches the bottom of the trail at 100 ft, the biker can then ride around the hill to the chairlift, which is also at 100 ft above sea level. This ride from one side of the hill to the other has no elevation change and, therefore, no slope.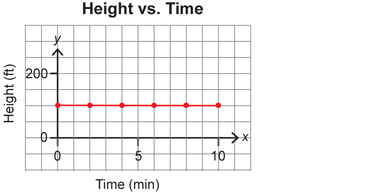
Two points on this graph include (0, 100) and (6, 100).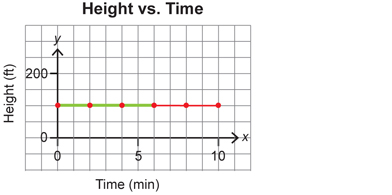
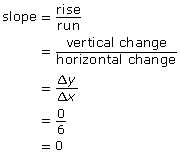
- an undefined slope
In this example, it does not work to have a vertical line. This would mean that time stands still (since time is along the x-axis). You would need to have a change in distance without a change in time.
If you graphed this impossible situation, the graph would look like this.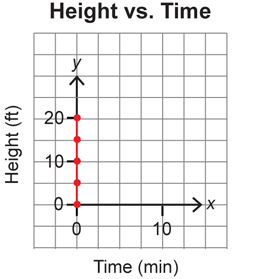
Two points on this graph include (0, 0) and (0, 20).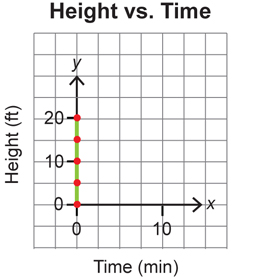
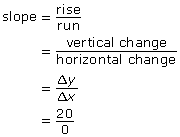
The slope is undefined, as you cannot divide by zero.
At this time, go to the multimedia DVD and open the “Unit 3 Project.”
 Going Beyond
Going Beyond

© abstrand/shutterstock

© Chepe Nicoli/shutterstock
In the Discover section of this lesson you completed a Math Lab based on the rise and run of stairs. The use of stairs is an ancient innovation used by the Mayan, Aztec, and Inca civilizations. Choose a step pyramid from one of these civilizations to investigate. You may find the Pyramids of Mesoamerica website helpful. Go to a search engine and type the keywords “pyramid Mesoamerica.”
The history of the pyramids provides a little insight into the cultures that created them. Research the history of your chosen pyramid, and see if you can find the measurements of the stairs.
- If the steps of a typical pre-Columbian period are 9 in high and 6 in wide, how does the slope of these stairs compare to the slope of modern stairs?
- Why would the stairs on an Aztec pyramid be steeper than those found in a current building?
Module 4: General Relations
Lesson 4 Summary
In this lesson you examined the following questions:
-
How can slope be used to describe the properties of objects?
-
Why is it possible to use any two points to determine the slope of a line?
The slope of a line is the measure of the line’s steepness. In this lesson you learned that you can interpret slope in three equivalent ways:

Slope can have positive or negative values, and slopes can also be equal to zero or they can be undefined. The slope of a line depends on its orientation. Specifically, this includes the following:
-
Lines rising to the right have a positive slope.
-
Lines falling to the right have a negative slope.
-
Lines parallel to the x-axis have a slope of 0.
-
Lines parallel to the y-axis have a slope that is undefined.
Throughout this lesson you saw how slope is applied in the construction of everyday objects. Slope is a major consideration in the building of stairs (both ancient and modern), ramps, and roofs. Slope is also a major factor for engineers who are responsible for designing Olympic event courses from ski jumping and bobsled racing in the winter to mountain biking and BMX racing in the summer. You may have discovered during this lesson that there are other words to describe slope such as grade, pitch, and incline. These expressions all describe the steepness of an object.
You also learned that you can calculate the slope of a line by determining the rise and run between any two points on a line. The reason for this is that the slope of a line is constant. You verified this by comparing the slope of a staircase, one step in the staircase, and consecutive steps in a staircase. The formula for the slope of a line given two points on the line with coordinates (x1, y1) and (x2, y2) is
![]() where m is the slope
where m is the slope
In Lesson 5 you will look at how you can use the slope of a line to find additional points on the line or to draw the line itself on the Cartesian plane. You will also investigate slope as a rate of change and explore how the slope of a line applies to real-world problems.