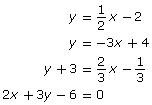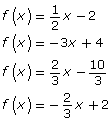Lesson 1: Function Notation
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 1: Function Notation |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:25 AM |
Module 6: Linear Equations
Lesson 1: Function Notation
Focus

man: © Scott Griessel/20972268/Fotolia; family: Getty Images/Comstock/Thinkstock
If you like to play music and you also like video games, you may enjoy playing a music video game. These games allow you to play popular music on game controllers designed to look and feel like real musical instruments including guitars and drum kits. Some of these games also come packaged with a microphone for singing along. Whether playing an instrument or singing a solo, players attempt to match the song notes that scroll on the video screen.
Every time you finish playing a song, the game displays your score as a percentage of the total number of notes that were played correctly. Reviewers of such games have indicated that they are entertaining, challenging, and fairly realistic. All video games are designed to allow the user to provide inputs into the game that result in output action on-screen.
The success of music video games comes from the fact that the games give the user a wider variety of inputs and combinations of inputs that result in an experience that closely approximates playing an otherwise complex song on a real instrument. For example, each drum pad emits a different sound, whether it is that of a bass drum, a cymbal, or tom. When a guitar is strummed, the tone that is heard depends on the fret buttons that are pressed. Inputs can be a single tap on a drum pad or simultaneous taps on two drum pads at different rates.
In the previous module you began your study of functions. You learned that a function is a relation between an input value (often called x) and the related output value (often called y). Each function has its own rule, and there is only one possible output value for any input value.
In this lesson you will learn a new way to represent a linear function known as function notation. In any function, there is a single output for every input. Function notation emphasizes the input/output property of functions.
Outcomes
At the end of this lesson, you will be able to
-
express the equation of a linear function in two variables using function notation
-
express an equation given in function notation as a linear function in two variables
-
determine the related range value, given a domain value for a linear function; e.g., if f(x) = 3x − 2, determine f(−1)
-
determine the related domain value, given a range value for a linear function; e.g., if g(t) = 7 + t, determine t so that g(t) = 15
-
sketch the graph of a linear function expressed in function notation
Lesson Questions
-
How do you sketch the graph of a linear function expressed in function notation?
-
Why are different types of notation used in mathematics?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 6: Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Use the “Linear Functions Terminology” applet to fine-tune your understanding of the vocabulary of linear relations, functions, and equations.
---------------------------------------
Work through the “Relations and Functions” interactive lesson to review the difference between relations and functions.
---------------------------------------
Watch the video “Graphing from Slope Intercept form” to review how to graph linear functions in slope-intercept form. Focus on how the slope is applied to find the second point.
----------------------------------------
Go to the following site to watch a video on Converting linear forms.
Module 6: Linear Equations
Discover
In this part of the section you will study some mathematical expressions.
 Try This 1- 3
Try This 1- 3

Reprinted by permission of the Royal Canadian Mint and the Bank of Canada.
Complete the following in your course binder.
This lesson will explore a new kind of notation for functions called function notation. Perform an Internet search to see if you can discover the following:
-
Which of the expressions in TT 1 could be interpreted as function notation?
-
How is function notation different from standard notation?
Record the information you find as well as the source of the information—in other words, record the URL address of any relevant web pages.
Possible TT1 -3 Solutions
In the next part of this section, you will answer some questions based on a graph that shows a bank account balance over 12 months.
Later in the lesson, you will be asked the same questions in a different way. You will need to revisit these questions to make comparisons.
 Try This 4 - 8
Try This 4 - 8
Complete the following in your binder.
Use the link below to check your answers to Try This 4 - 8.
Module 6: Linear Equations
Explore

iStockphoto/Thinkstock
Some people enjoy songwriting or music composition as a way to spend leisure time. If you have a talent for writing lyrics or composing tunes, this can be a rewarding pursuit. It’s really easy to record your composition using computer software that simulates any number of instruments.
There is a special way to write music. The notation that is used in music involves symbols representing notes. A particular symbol reveals many things about how the note is to sound. For example, the position of the note indicates the pitch of the sound. The appearance of the note may reveal that the sound should be sustained for a long time or played rapidly in succession with another note. Notation in musical composition also tells you the rhythm of the piece and which set of notes will be used.
Have you ever watched musicians play music while reading the notes off of a sheet? That they can do it smoothly is a reflection of the fact that the system of notation for music is efficient. Similarly, in mathematics, functions can be represented in function notation. This type of notation emphasizes the input-output nature of functions and can be an efficient way of evaluating functions and reporting particular values on the graph of a function.
In this lesson you will write functions in another way—using function notation.
Glossary Terms
Add this term and its definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate the term as well
-
function notation
---------------------------------------------------------------------------------------------------------------
Standard Notation vs Function Notation
Examine the following chart comparing equations expressed in standard notation and in function notation. Four different linear equations are shown in the left-hand column. The right column shows the same equations expressed using function notation. Compare the two columns and identify the key difference.
|
Standard Notation |
Function Notation |
|
|
|
You may have noticed that the key difference is that in function notation, f(x) replaces y. You may have also noticed that in function notation, the f(x) is always isolated. For instance, it is not appropriate to express a function as ![]()
 Try This 9 - 12
Try This 9 - 12
Use what you have discovered about the relationship between standard notation and function notation to complete the following questions below.
Complete the following in your binder.
TT 9. Express the equation of each linear function using function notation.
a. y = x + 1
b. x + 4y + 8 =0
TT 10. Express each equation in function notation as a linear function in two variables. The form of standard notation is indicated in each case.
a. f(x) = -3/4x + 1 ( Slope-intercept form)
b. f(x) = 2x -9 (general form)
Possible TT9-10 SolutionsUnlike standard notation, function notation gives names to functions. Usually, f(x) is used to represent the dependent variable when the situation does not indicate a particular context. The notation also shows the input value and the process by which the input is turned into a single output value.
The next example asks questions relating to a linear function as expressed using function notation. See if you can answer these questions before reading the solutions.
 Tips
Tips
Function notation is used to describe functions only. Relations that are not functions should not be represented with function notation.
Example
Consider the function given as f(x) = −3x + 4.
- What is the name of the function?
- How do you say the expression? What does it mean?
- Determine f(2).
- Determine the value of x when f(x) = −11.
Solution
- The name given to the function is f. Similarly, the name of the function g(x) = x is g and the name of the function h(x) = x2 + 4 is h.
- The expression can be read in different ways:
- f at x is equal to −3x + 4
- f of x is equal to −3x + 4
- f as a function of x is −3x + 4
- The expression f(2) means the “output of the function f when the input value is 2.” Note that in f(2), x has been replaced with 2. Therefore, you can make the same substitution on the right side of the equation.
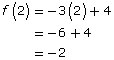
- The expression f(x) = −11 means that the output is −11. Your task is to find the value of x, or the input, under this condition. Here, you can replace f(x) with −3x + 4.
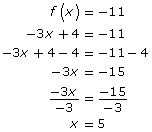
Module 6: Linear Equations
 Self-Check
Self-Check
After working through the Example problems, test your level of understanding by answering the following questions.
SC 1. If f(x) = 5x + 2, what is f(2)?
SC 2. If g(x) = −3x, what is g(−2)?
SC 3. If f(x) = −2x + 3, what is f(3)?
SC 4. If g(x) = −3x, what is x if g(x) = −18?
SC 5. If f(x) = 5x + 2, what is x if f(x) = −13?
SC 6. If g(x) = −2x + 3, what is x if g(x) = −2?
Recall that a function is a relation where each “input” value only has a single “output” value. Other input values may have identical output values as this function, but the important idea is that each input has only one output value.
Generally speaking, function notation is represented in this way:
f(input value) = output value
Another way of saying this is f(domain) = range.
The following is the graph of ![]() . Remember that this is equivalent to
. Remember that this is equivalent to ![]()
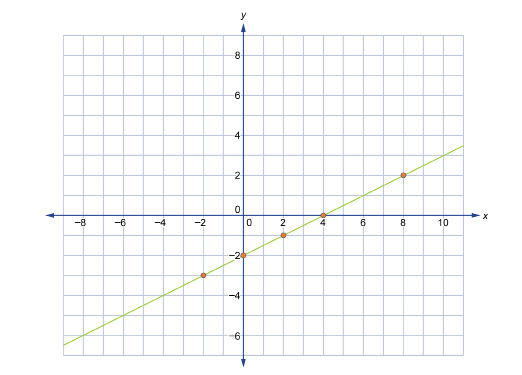
Recall that the line represents the linear function. Each point on the line is an ordered pair that satisfies the equation of the line. On this graph, the point (8, 2) has an x-coordinate of 8 and a y-coordinate of 2. In function notation, this relationship is expressed as f(8) = 2.
 Try This 11 - 13
Try This 11 - 13
Complete the following in your binder.
Use the link below to check your answers to Try This 11 - 13.
---------------------------------------------------------------------
The symbol most commonly used to denote a function is f because function starts with f, but you may use other letters to express a function.
Consider the following example.
The formula for the circumference of a circle is ![]()
Circumference is a function of the diameter. So, to express the formula in function notation you may want to use the letter C instead of f.
The formula expressed in function notation is ![]() Read this as “C as a function of d is
Read this as “C as a function of d is ![]() ” or “C of d is
” or “C of d is ![]() ”
”
 Think
Think
Can you think of other formulas that could be expressed in function notation?
 Read
Read
Function notation is useful when applied to word problems. When this happens, you will see that the letter assigned to the function may not be f and will likely be a letter that is more suited to the variable it represents.
You will now work through an example in your textbook to see how function notation is used to determine values in a given context. As you do so, focus on two questions:
- How are letters chosen to represent both the independent and the dependent variables?
- How do you know whether you are supposed to evaluate the independent variable or the dependent variable?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Using Function Notation to Determine Values” on pages 269 and 270.
Graphing a function expressed in function notation is identical to graphing the same function expressed in standard notation.
 Try This 14
Try This 14
Print (or copy by hand) and complete the following in your binder.
Try This 14 Questions
Use the link below to check your answers to Try This 14.
Possible TT14 (Try This 14) Solutions
--------------------------------------------------
 Read
Read
Go to your textbook to see how you can sketch a linear function expressed in function notation. Compare the strategy used in the textbook with the strategy you used in TT 14.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Sketching a Graph of a Linear Function in Function Notation” on page 315.
The example shows how you can determine two points on the graph. What is special about these two points? How is function notation used to determine these points? What other strategies could you use to sketch the graph?
 Self-Check
Self-Check
In this lesson you have learned how to interpret, express, and use linear equations written in function notation. Revisit the questions posed in TT 4 to TT 8 earlier in the lesson.
SC 7. Go to “Module 6: Lesson 1: SC 7.” Match TT 4 to TT 8 to the equivalent questions expressed in function notation.
-------------------------------------
 Watch and Listen
Watch and Listen
Before finishing the lesson with some practice, watch this helpful video on Function notation. Note that on the left side of the screen, there are links to the practice questions and on the right, there are links to other sites.
--------------------------
 Try This 15
Try This 15
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 15. a. Complete “Exercises” questions 6.a), 6.c), 7.b), 7.c), 14.a), 14.d), 15.b), and 19 on pages 271 and 272.
b. Complete “Exercises” question 16 on page 296.
c. Complete “Exercises” questions 6.a) and 15.a) on pages 319 to 322.
--------------------------------------------------
Watch the following video titled “What Is Function Notation?” This video summarizes the key points of this lesson. You will see how function notation is both interpreted and applied. ** You may need to click above the words in the white space to activate the video**
Module 6: Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

Hemera/Thinkstock
An important skill for any musician is the ability to sight read music. Sight reading involves the reading and performing of a piece of music without the benefit of having seen it before. There are many benefits of sight reading, not the least of which is the fact that a musician can become more fluent with the language or notation of music. In this project, you will engage in a sight-reading simulation. Don’t worry—you won’t have to learn how to play a musical instrument to do this project.
Now, go to the Unit 4 Project and complete the Module 6: Lesson 1 component of the project.
 Going Beyond
Going Beyond
© caraman/12535393/Fotolia
A function is sometimes compared to a machine. A function takes an input value and processes it into an output value. Similarly, a machine such as a household clothes dryer takes wet clothes (the input) and processes them into dry clothes (the output).
In a typical household, you will also find a machine that reverses the process of a dryer. This machine will take dry clothes and process them into wet clothes. Do you know what machine does this? Hint: The machine is in the illustration. In this Going Beyond section you will explore functions that will reverse the process of a given function.
-
Graph the function f(x) = −2x + 6.
-
Evaluate f(1) by looking at the appropriate point on the graph on f(x).
-
Graph the function
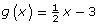 on the same set of axes that you used to graph f(x).
on the same set of axes that you used to graph f(x).
-
Evaluate g(8) by looking at the appropriate point on the graph of g(x).
-
Compare your answers to questions 2 and 4. How are the two points related?
-
Look for other points on the graphs of f(x) and g(x) that are similarly related.
In mathematics, functions such as f(x) and g(x) are known as inverse functions. You may have the opportunity to study inverse functions in subsequent courses.
Save your graphs and results in your course folder. Your teacher may review your work at a later time.
Module 6: Linear Equations
Lesson 1 Summary
In this lesson you investigated the following questions:
-
How do you sketch the graph of a linear function expressed in function notation?
-
Why are different types of notation used in mathematics?
At the beginning of this lesson, you were introduced to a new way of expressing functions called function notation. Like other forms of notation used in mathematics, function notation uses an arrangement of symbols to indicate a process. You learned that f(x) replaces y in a linear equation and that function notation is reserved only for functions. You learned that f(x) does not mean “f times x”, but is read as “f of x” or “f at x.” You learned that function notation can be used as an efficient way of defining points on a graph. In the Reflect and Connect section of the lesson, you explored standards of mathematical notation. You may have learned that mathematical notation makes a concept easier to describe and understand.
In this lesson you learned that sketching a line expressed in function notation is exactly the same as sketching a line expressed in standard notation. The benefit of using function notation is that it is more efficient. With function notation, for example, you can say “plot f(2)” instead of “plot the point with x-coordinate equal to 2.”
In the remainder of this module you will see function notation used to express the equations of linear functions. Function notation will be particularly helpful in the last lesson where you will assign meaningful letters to functions in problem-solving contexts. You will continue to use function notation in your future math courses.