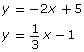Lesson 2: The Equation of a Line
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 2: The Equation of a Line |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:28 AM |
Module 6: Linear Equations
Lesson 2: The Equation of a Line
Focus

© Irmina Mamot/1634365/Fotolia
Scuba diving has become a popular leisure activity, especially for people who are on holidays in tropical places. Scuba is short for self-contained underwater breathing apparatus. While it is fun and thrilling, scuba diving can be a dangerous activity without the proper training. Scuba diving courses emphasize safety and devote much attention to the mastery of basic skills as well as the execution of emergency procedures.
Decompression sickness, commonly referred to as “the bends,” is caused by rising to the surface too quickly after a prolonged stay in deep waters. With the bends, so called because the pain would cause divers to bend over, tiny bubbles of gases normally dissolved in the blood form in the joints, similar to the tiny bubbles that form in a soda bottle when you open it. If you shake a soda can and then open it quickly, many bubbles will form due to the change in pressure when the can is opened. This is similar to decompression sickness. Fortunately, understanding the relationship between depth and pressure allows scuba divers to take actions to avoid getting “the bends.”
As divers descend to lower depths in the ocean, the ambient pressure—the pressure of the surrounding water—on them increases at a linear rate. At sea level, the pressure is 101.3 kPa, and each 10 m of depth adds another 101.3 kPa of pressure.
Outcomes
At the end of this lesson, you will be able to
-
write the equation of a linear relation, given its slope and the coordinates of a point on the line, and explain the reasoning
-
write the equation of a linear relation, given the coordinates of two points on the line, and explain the reasoning
Lesson Questions
-
How are the properties of a linear function used to determine its equation?
-
In what ways does drawing a graph help you to solve math problems?
 Assessment
Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 6: Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
--------------------------------------
Review how to find the slope from two points using the slope formula.
------------------------------------
Use the “Slope-Intercept Form: y = mx + b” video to review some of the concepts for how to find the equation of a line.
Go to “Determining the Equation of a Line.”
------------------------------------------
Use the “Graphing Linear Equations Using the "Linear Function Explorer” interactive
applet to review how the equation of a linear relation in slope-intercept form relates to its graph.
---------------------------------------------
You have learned three forms for expressing a linear function. These are summarized in the following table.
|
Name |
Form |
Examples |
|
slope-intercept |
|
|
|
slope-point |
|
|
|
general |
|
|
 Read
Read
Go to your textbook to review how you can convert a linear equation in general form. As you do, try to find out the answers to the questions:
-
How do you know which number by which to multiply each term?
-
How do you know which side to collect the terms?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Rewriting an Equation in General Form” on page 379.
Module 6: Linear Equations
Discover
 Math Lab: Exploring Lines
Math Lab: Exploring Lines
Complete the Math Lab: Exploring Lines.
Math Lab: Exploring Lines
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder.
Module 6: Linear Equations
Explore

© Galyna Andrushko/1472722/Fotolia
Mountaineering is a recreational pursuit that takes physical endurance and determination. Just as you can experience sicknesses due to rapid pressure changes in the depths of the ocean, you can also become sick at high altitudes. Altitude sickness, also called acute mountain sickness (AMS), is a condition that affects individuals whose bodies cannot take in enough oxygen at high altitudes. This condition occurs when the person does not allow time for his or her body to acclimatize to the diminished levels of oxygen at higher elevations. Experienced mountaineers will adopt a “two steps forward, one step back” approach to climbing. In other words, during the day the mountaineer will climb to higher elevations to push his or her bodies to adapt, but then at night the mountaineer will climb back down to base camp to sleep. Subsequently, the mountaineer will progressively climb to a higher elevation and then climb back down to a slightly higher base camp than the previous one.
Another effect of higher altitudes is that the boiling point of water is reduced. In fact, the relationship between the altitude and the boiling point is linear. For example, the normal boiling temperature of water is 100°C, but at 4000 m elevation, that critical temperature is closer to 86°C. So the next time you go mountain climbing, you can expect to eat your morning oatmeal a little sooner because you won’t be waiting as long for the water to boil!
 Did You Know?
Did You Know?
The higher the temperature, the faster food cooks. Even though water boils sooner at higher altitudes, food actually takes longer to cook! This is because the temperature of the boiling water is lower.
Glossary Terms
Add this term and its definitions to the Glossary Terms in your notes. You may also want to add examples that demonstrate how each term is applied.
-
linear equation
-----------------------------------------------------------------------
The approach to the determination of the equation of a line depends on the information that is provided. The equation of a line can be determined as long as you have two pieces of information: the slope and a point on the graph.
Recall from Lessons 3 and 4 of Module 5 that there are three forms for the equation of a linear function:
-
slope-intercept form
-
slope-point form
-
general form
You will find that the first two forms in the list are more practical to use when determining the equation of a line. However, you can still convert an equation written in slope-intercept or slope-point form into general form.
Generally speaking, when you are asked to write the equation of a line, you will be given either of the following:
-
the slope of the line and the coordinates of a point on the line
-
two coordinates points on the line
You have previously learned how to write the equation of a line in the form y = mx + b when you are given the slope, m, and the y-intercept, b.
In this lesson you will investigate how to write the equation of a line when given different information about the line.
-------------------------------------------------
Determining the Equation of a Line: Given Slope and Point
There are ways to write a linear equation when given its slope and a point on the line. This following video clip shows one method, and the example after the video clip shows an alternate method.
 Watch and Listen
Watch and Listen
View the video titled “Linear Equation Given Slope and One Point.” Watch for the two equivalent versions of the equation at the end of the video. Can you convert the original equation into those two forms?
-----------------------------------
Consider another approach to finding the equation of a line when given the line’s slope and a point on the line. This approach is a graphical one. The next example shows how you can determine the equation of the same line that was presented in the video. As you work through the solution, see if you can detect both advantages and disadvantages in the method.
Example
Use a graphical approach to determine the equation of the line with a slope of ![]() that passes through the point (12, 8).
that passes through the point (12, 8).
Solution
Plot the point (12, 8). Apply the slope of ![]() by rising up 1 unit and moving 4 units to the right. The second point will be plotted at (16, 9). Optional: You can get a third point by applying the slope of
by rising up 1 unit and moving 4 units to the right. The second point will be plotted at (16, 9). Optional: You can get a third point by applying the slope of ![]() in a different way. You do this by dropping 1 unit and moving 4 units to the left of (12, 8). The new point will be located at (8, 7).
in a different way. You do this by dropping 1 unit and moving 4 units to the left of (12, 8). The new point will be located at (8, 7).
Join the points with a line.
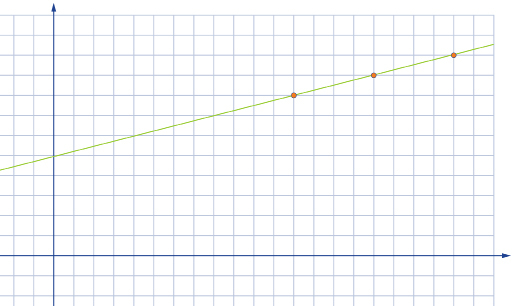
From the graph, you can see that the y-intercept is (0, 5). Since the slope is ![]() and the y-intercept is b = 5, the equation is
and the y-intercept is b = 5, the equation is ![]()
 Share 1 - 3
Share 1 - 3
Review your answers to the Math Lab. Working with a partner ( if possible), respond to the following questions.
1. a. How is your approach similar to and different from the one presented in the example provided in the lesson?
b. How is your approach different from the one presented in the example provided in the lesson?
2. What advantages does a graphical approach have to finding an equation?
3. a. What drawbacks are there in using a graphical approach?
b. Does the use of a graph to determine the equation of a line work in all instances?
 Read
Read
Go to your textbook to work through an example that shows how you can write the equation of a line when given the slope and a point on the line.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Writing an Equation Using a Point on the Line and Its Slope” on page 368.
Not all equations are going to have integral coefficients. Some, as in this example, may have rational coefficients. Study carefully how the y-intercept, which is a fraction, is determined.
 Self-Check
Self-Check
SC 1. Find the equation of a line, given m = −2 and the y-intercept = 4.
SC 2. Find the equation of a line in slope-intercept form, given that the slope is −3 and the line passes through (4, 6).
SC 3. If given slope ![]() and coordinates C(2, 6), what is the equation of this line in slope-intercept form?
and coordinates C(2, 6), what is the equation of this line in slope-intercept form?
SC 4. Find the equation of the line of slope ![]() and the y-intercept (0, 3).
and the y-intercept (0, 3).
 Try This 1
Try This 1
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” question 5 on page 372. Write the equation in slope-point form; then convert to slope-intercept form and general form.
Use the link below to check your answers to Try This 1.
Possible TT1 Solutions
Explore 2
Determining the Equation of a Line: Given Two Points
In mathematics, there are many different ways of solving the same question. It is important that you develop problem-solving strategies that suit you—no two people think in exactly the same way..
 Try This 2
Try This 2
Complete the following questions in your course folder ( binder).
TT 2. a.Develop a strategy for writing the equation of a line when given two points. (Hint: Is there a way to determine the slope of the line?)
b. Demonstrate how this strategy can be applied to the following exercise. Write the equation of a line that passes through the points (–2, 1) and (1, 7). Express your answer in slope-intercept form as well as general form.
 Watch and Listen
Watch and Listen
Watch the “Linear Equation Given Two Points” video, and compare your strategy in TT 2 to the strategy suggested in the video. Also, see if your answers match the answers presented in the video.
---------------------------------------------
 Try This 3
Try This 3
Based on what you have seen in the video clip, complete TT 3 in your course folder (binder).
Answer the questions based on what you have seen in the video titled “Linear Equation Given Two Points” and your own results.
TT 3. a. How did your strategy compare with the strategy presented in the video? Were they exactly the same? If so, what is your rationale for using this strategy? If not, how did you arrive at the correct answer?
b. Two points are given in the question, but only one point was used to determine the equation of the line. Did you use the same point as was used in the video? If so, try the other point to see if it would yield the same equation. If not, what conclusions can you make about which point should be used?
 Read
Read
Go to your textbook to work through an example that demonstrates how to determine the equation of a line when given two points on the line.
Foundations and Pre-calculus Mathematics 10 (Pearson)“Example 3: Writing an Equation of a Linear Function Given Two Points” on pages 369 and 370 shows a variation of the approach used in the video titled “Point-Point Equation of a Line.” Before you read the example, make sure you read the preamble at the top of page 369. Then, as you read the example, focus on the green writing in the solution, which gives a rationale for each step. |

Use the link titled “Finding the Equation of a Line” to practice writing equations of linear functions. They start out very simple and then get more complicated. No solutions are provided, just a mark, but it is good practice.
-----------------------------------------------------
 Watch and Listen
Watch and Listen
It’s play time!
Click on “Deep Sea Diver” . You will navigate the depths of the sea as a scuba diver. Collect the gems and evade the jellyfish, sharks, and whales. Don’t forget to go to the buoys at the surface for air!
In order to progress through the levels, you will have to answer multiple choice questions correctly. All of these questions deal with the concepts learned in this lesson. You will receive rewards to help you each time you answer a question correctly. Good luck!
Hint: In this game, you will encounter the expression standard form. You may want to review your glossary terms from Module 5: Lesson 4 to recall what this means.
 Self-Check
Self-Check
Now that you have worked through an interactive lesson and played a game relating to writing linear equations, here is an opportunity for you to demonstrate what you have learned. For each of the following questions, show the steps that you would follow to obtain the equation. You may use either an algebraic or graphical approach.
SC 5. In slope-intercept form, write the equation of the line that passes through the following points:
- (0, 4) and (2, 0)
- (2, 4) and (6, 6)
- (−2, 1) and (1, −4)
 Try This 4
Try This 4
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 4.a. Complete “Exercises” question 11 on page 372.
b. Complete “Review” questions 18 and 19 on pages 389 and 390.
Use the link below to check your answers to Try This 4.
Possible TT4 Solutions
Module 6: Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

Photos.com/Thinkstock
Have you ever wanted to go on a tropical vacation? There are some travel agencies that will send you on a scuba diving tour, complete with return airfare, accommodations at a resort, diving lessons, and many opportunities to explore the undersea world. You can study the beautiful colours and textures of the flora and the fauna in tropical waters or, if you are more adventurous, you can explore a shipwreck!
Go to the Unit 4 Project and complete the Module 6: Lesson 2 portion of the project.
 Going Beyond
Going Beyond
Often in mathematics, it is essential to learn how to solve a problem using a strategy that is not necessarily the quickest way to the solution. The reason for this is because the selected strategy is the easiest to understand or makes use of those principles with which the learner might be most familiar.
When you are learning something new, what disadvantages are there in learning a shortcut immediately?
Once you understand how a process works, you may adapt the process to enable you to arrive at the answer more quickly or with less work.
In this lesson you learned to write linear equations when given either of the following:
-
a slope and a point
-
two points
In this section you will develop “shortcut” strategies for determining the equation of a line in slope-intercept form when certain information is known.
Complete the chart in the “Shortcut Strategies” activity. For each set of given information in the chart, there are two examples provided. Feel free to construct and analyze your own examples, as long as they also provide the same initial information.
Module 6: Linear Equations
Lesson 2 Summary
In this lesson you investigated the following questions:
-
How are the properties of a linear function used to determine its equation?
-
In what ways does drawing a graph help you to solve math problems?
In this lesson you learned how to use given information to write the equation of a line. You used both the slope-intercept form and the slope-point form of a linear function to write linear equations. You learned that, in order to write the equation of a line, you need to know certain properties of the line. These properties are its slope of the line and a point through which the line passes. Sometimes you are not given a slope but only two points. In these cases, you can use the slope formula to determine the slope of the line. You watched videos and worked through interactive lessons that demonstrated how to determine the equation of a line.
In this lesson you compared two methods of identifying the properties of a linear function—graphically and algebraically. You may have discovered that it is easier in some instances to determine the properties of a line by sketching a graph. A graph can be a rich source of information about a math problem. A graph readily gives you a slope and the y-intercept. These values can then be used to determine the equation of the line in the form y = mx + b. The steepness of the line gives an indication of the rate of change of one variable with respect to another. The scale of each axis gives you an idea of the size of the quantities in the context of the problem.
While a graph can be helpful to you when solving problems, you may have also discovered that it is sometimes easier to determine a line’s properties algebraically. For example, when the y-intercept of a line is not an integer, it is much easier to determine its exact value algebraically as opposed to graphically.
In the next lesson you will examine the relationship between parallel lines. You will also examine the relationship between perpendicular lines. You will analyze their slopes and write equations of lines which are parallel or perpendicular to given ones.