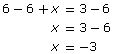Lesson 4: Applications of Linear Equations
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Applications of Linear Equations |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:25 AM |
Module 6: Linear Equations
Lesson 4: Applications of Linear Equations
Focus

© Antonio/18182725/Fotolia
This image is symbolic of music piracy or illegal downloading of music files.
In the late 1990s, websites emerged that enabled users to share their digital music files. The technology was easy to use and it was also a way for people to update their music collection for free. As a result, the music stores experienced a decline in CD sales. In turn, music artists, who were not compensated by this type of practice and who also suffered losses in royalties due to the drop in retail sales, launched lawsuits against the companies overseeing these websites. Ultimately, as more artists joined the fight, these websites were deemed to be in violation of copyright laws. These lawsuits resulted in the shutdown of such websites. Nevertheless, these events revolutionized the way that music and movies are purchased or rented today.
There are now many legitimate websites that offer a vast collection of songs, albums, and films for purchase. Consumers can buy songs, which can be purchased individually or as part of a whole album, that cost less than $2.00 each. Movies, too, can be rented or purchased online for approximately the same amount as one would pay in a video rental outlet. In this way, the music artists and movie producers are assured of their royalties. While they may not receive the same amount for the sale of a single song as they would have in the past for the sale of an entire CD, this may be balanced by the fact that the songs are now available to a wider audience thanks to the Internet.
Unfortunately, despite low prices and widespread availability, music is still being stolen by criminals who engage in an activity known as piracy. Piracy is the unauthorized reproduction or distribution of copyright-protected media such as digital music and movie files. These criminals illegally copy music and movies onto CD, DVD, or Blu-Ray media, and then sell them on the black market for a fraction of the cost of the same content available from legitimate retailers.
In this lesson you will bring together what you have learned in Lessons 1, 2, and 3 and then apply your skills with linear equations to practical problem-solving situations centred on the enjoyment of music. You will continue to work with linear equations expressed using both standard and function notation. You will focus on the use of linear equations to model different scenarios. You will also learn how to interpret the different parts of a linear equation in a given context.
Outcomes
At the end of this lesson, you will be able to
-
graph linear data generated from a context, and write the equation of the resulting line
-
solve a problem, using the equation of a linear relation
Lesson Questions
-
How are the fixed and variable elements of a problem related to the linear equation y = mx + b?
-
How do you apply techniques and concepts learned in this module to solve problems?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 6: Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Watch the video titled “Graphic Representations.” The video shows an example of how you can interpret the independent and dependent variables in a given context. As you watch, focus on where the independent variable and dependent variable are placed on a graph. You have viewed this video clip when you worked on Module 4.
-----------------------------
To review slope as a rate of change, you may want to revisit the work that you did in Module 4: Lesson 5. Work through the last Watch Sal Khan work through a number of examples on “Slope as a Rate of Change.”
---------------------------------------
Watch this helpful video on Function notation. Note that on the left side of the screen, there are links to the practice questions and on the right, there are links to other sites.
---------------------------------------
The basic rule used in solving equations in algebra is to balance both sides of the equation. In other words, what is done to one side of the equation must be done to the other side of the equation as well. For example, if you add a term on the left side, you must add the same term on the right side. If you multiply a term on the left side, you must multiply the same term on the right side. The following table shows how you can solve two different linear equations.
|
Solving a Basic Equation |
Solving by Combining Like Terms |
|
In the equation 6 = 3 − x, you want to get the x on the left side and the other items on the right side.
First, add x to both sides of the equation.
6 + x = 3 − x + x 6 + x = 3
Next, subtract 6 from both sides of the equation.
By following these two steps, you learn that x = −3, which is the solution to the equation. |
Consider the equation 2x + 3 = −4x − 7.
You can solve the equation by first getting all the x terms on the left side.
Add 4x to both sides.
2x + 4x + 3 = −4x + 4x − 7
Combine like terms.
6x + 3 = −7
Subtract 3 from both sides.
6x + 3 − 3 = −7 − 3
Combine like terms.
6x = −10
Divide both sides by 6.
Simplify the fraction.
|
Try the “Algebra Four!” equations game to practise your equation solving skills. ou can choose different types of questions to practise. Select “Two-Step Problems” and then play one round. Next, you can add “Variable on Both Sides” the second time you play. This game is best played with two people, so you may want to invite a classmate to play with you or perhaps your teacher or a parent may be willing to play with you. If you feel up to the challenge, you can select the first, second, and fourth options. (Do not select the “Quadratic” option as you will be learning how to solve quadratic equations in a future course.) As a warning, if you try the game, you may need to have a piece of paper and a pencil handy!
-----------------------------
Materials
You will need the following items in order to complete Math Lab: Counting Beats.
- CD or MP3 player
- music CD or MP3 song
- stopwatch or timepiece
Module 6: Linear Equations
Discover

iStockphoto/Thinkstock
Ever wonder what it would be like to be the music deejay that plays the songs at the dances? Nowadays, with the advent of personal music players and computer software, it is easy for almost anyone to do what deejays used to do with only a couple of turntables, a mixer, and a collection of records. One skill for the traditional deejay was to be able to mix two pieces of music. In other words, as one song neared its conclusion, the deejay had to start another song in a way that maintained continuity to the flow of songs. In order blend songs like a pro, you need to match the tempos of the outgoing track and the incoming track.
In the Math Lab that follows, you will analyze the tempo of your favourite songs by calculating the beats per minute.
 Math Lab: Counting Beats
Math Lab: Counting Beats
Go Math Lab: Counting Beats,and complete it.
Math Lab: Counting Beats
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder.
Math Lab Answers
Module 6: Linear Equations
Explore

Hemera/Thinkstock
A smartphone is a device that serves multiple functions. Many smartphones are not only cellphones but are also personal organizers, cameras, voice recorders, and portable media players with the ability to access the Internet. Used largely by those in the business world initially, smartphones have gained popularity with many people on the go. These devices offer its users GPS navigation, instant weather reports, e-readers, games, restaurant reviews, stock reports, and other applications.
Smartphones offer many conveniences, but they are not free. There is an initial fee and a subsequent monthly fee, depending on the plan that is purchased. The initial fee covers the cost of the device and varies depending on the length of the contract. The monthly fee depends on the options that are selected and the amount of time spent using the device. For example, you may be charged for how long you spend using the smartphone to surf the Internet. The cost of using a smartphone can be modelled by a linear function.
In this lesson you will model and solve problems using linear equations.
Glossary Terms
Add these terms and their definitions to your Glossary Terms section in your noted. You may also want to add examples that demonstrate how each term is applied.
- fixed term
- variable term
-----------------------------------
You already know that the equation of a linear function can be expressed as y = mx + b. This equation can also be expressed in function notation as f(x) = mx + b. When solving problems, you may want to choose meaningful letters to represent the independent and the dependent variables. For example, a distance-time problem could be represented by the letters d and t.
 Try This 1 - 3
Try This 1 - 3
Complete the following in your binder.
TT 1, TT 2, and TT 3 provide descriptions of linear scenarios.
Identify the independent and the dependent variables, and select appropriate letters to represent them. Note: If you are still unsure about the terms independent and dependent, review the “Graphic Representations” video from the Refresher section of this lesson.
TT 1. As the cellphone usage increases, the cost also increases.
TT 2. A scuba diver swims in the depths of the ocean. The deeper she swims, the stronger the water pressure that is exerted on her body.
TT 3. A mountaineer climbs a very high mountain. The temperature drops with every kilometre he climbs.
Possible TT1-3 Solutions
 Read
Read
The linear problems that you will encounter will require you to do several things in sequence. Go to your textbook to look at the structure of different problems. Your focus is on what is being asked, not on the solutions. As you read, take note of what each part of the question requires.
Foundations and Pre-calculus Mathematics 10 (Pearson)
First, read “Example 4: Using an Equation of a Linear Function to Solve a Problem” on page 361. Next, read “Example 4: Determining an Equation from a Graph of Generated Data” on pages 382 and 383.
It is important to understand how problems are structured so that you know how to approach them. Look back at the structure of the Math Lab. Compare the order of the questions posed in the Math Lab and the same structure in the examples you have just read about in your textbook. Do you notice similar patterns? Why are the questions asked in that particular order?
 Try This 4 - 8
Try This 4 - 8
Complete the following in your binder.
You may need to go back to your textbook and review the examples you have just read to answer these questions.
TT 4. Are there similarities between what is required by the first textbook example and the second textbook example?
TT 5. What key phrase is common among the questions that are posed in the textbook examples?
TT 6. a. How are the questions structured?
b. In what order are the parts arranged?
TT 7. Why is the order of the parts important?
TT 8. What skills that you have previously learned will you need to recall or apply to answer each question?
Possible TT4 - 8 Solutions
 Watch and Listen
Watch and Listen
Watch the video “Write a Linear Given Fixed and Variable Costs” to get an idea for how to assign meaningful letters to variables and to learn how to solve a problem one part at a time. As you work through the lesson, pay attention to how the answer from each part is used to solve the next part of the problem.
-----------------------------
Here is a second example, showing the steps clearly as well.
-----------------------------
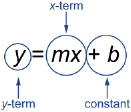
Analyzing the Parts of a Linear Equation
The slope-intercept form of a linear equation has three distinct parts as represented in the diagram shown.
 Try This 9-11
Try This 9-11

© fokinol/11851192/Fotolia
Complete the following in your binder.
Try This 9 - 11 Questions
Use the link below to check your answers to Try This 9-11.
Possible TT9-11 Solutions
The x-term in a linear equation is known as the variable term since it varies according to the independent variable. The constant is known as the fixed term since it remains the same regardless of the value of the independent variable.
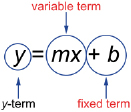
You can use the idea of the variable and fixed terms to translate descriptions of linear relations into equations. The part of the context that is constant—such as the CD wallet without CDs—is the fixed term. The part of the context that changes depending on the independent variable—such as the total mass of the CDs, which changes depending on the number of CDs—is the variable term.
 Self-Check 1 - 4
Self-Check 1 - 4
Test your ability to identify the fixed and variable terms in the description of a linear situation. Also, see how accurately you can determine a correct linear equation for a given situation. Choose meaningful letters for the variables.
SC 1. Mominah works at an electronics store. She is paid a base salary of $1500 per month. She also receives a 6% commission on her monthly sales. Write an equation relating Mominah’s sales and earnings for one month.
SC 2. A cellphone plan charges the customer $30 per month plus $0.25 per text message. Write an equation relating the number of text messages and the cost of the plan for one month.
SC 3. Madelyn enters a piano festival in which there are numerous categories. Each category takes 40 minutes to complete. At the end of the festival, there is a 90-minute concert for all competitors. Write an equation relating the amount of time Madelyn spends at the piano festival and the number of categories she enters.
SC 4. The temperature at a base camp is 4°C. For every 1000 m elevation, the temperature drops by 6.5°C. Write an equation relating the elevation to the temperature.
 Read
Read
By working through the Math Lab and by reading in your textbook, you may have observed that problems are easier to tackle when broken into separate parts. These parts may include the following:
-
identifying and assigning variables
-
sketching a graph
-
constructing an equation
-
using the equation to predict other values
Sometimes the questions you encounter will guide you through each part, and, at other times, you will have to decide how to structure your approach.
You will now return to the examples that you have previously read. This time, focus on the solutions. Specifically, try to discover what information is important to each part of the question and how the information that is generated in one part is used in subsequent parts.
Foundations and Pre-calculus Mathematics 10 (Pearson)
First, read “Example 4: Using an Equation of a Linear Function to Solve a Problem” on page 361. Next, read “Example 4: Determining an Equation from a Graph of Generated Data” on pages 382 and 383.
 Self-Check 5
Self-Check 5
SC 5. Four friends stop at a restaurant for its lunchtime pizza special. There is a base price for the pizza and a charge for each topping. Kaz ordered a ham-and-pineapple pizza and paid $10. Leona had the same size of pizza with pepperoni, mushroom, bacon, and black olives. She paid $15.
- Create a graph of cost versus number of toppings.
- What does the slope of the graph represent?
- What is the y-intercept, and what does it represent?
- Find the equation that represents this situation.
- Ramon had a pizza with five toppings. How much did he pay?
- Maggie has $24 to spend. What is the maximum number of toppings she could have?
 Try This 12
Try This 12
Complete the following in your binder.
Go to your textbook now to practise applying the concepts that you have learned.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 12. a. Complete “Exercises” questions 14 and 16 on page 363.
b. Complete “Exercises” question 16 on page 384.
Use the link below to check your answers to Try This 12.
Possible TT12 Solutions
Module 6: Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

Digital Vision/Thinkstock
Legal downloading has become an alternative to purchasing CDs to build your music collection. Some artists have started selling MP3s directly from their own websites. Sometimes up-and-coming artists offer a free song to help promote an album.
Your Project Connection for Lesson 4 is based on questions about a music downloading website. At this time, go to the Unit 4 Project and complete the Module 6: Lesson 4 component of the project.
 Going Beyond
Going Beyond

iStockphoto/Thinkstock
Modern technology has made it even more convenient for us to listen to music wherever we are and whatever we may be doing. You can listen to music while you are riding the bus, doing your homework, working out at the gym, or doing household chores. You can take your entire music collection with you. In fact, you can even add the latest songs to your Wi-Fi enabled portable media player.
Listening to your favourite music can be a great way to spend your leisure time; however, prolonged exposure to loud music can threaten your hearing. Tiny hair cells in the cochlea of your ear are the receptors for hearing. Signals from these hair cells are translated into nerve impulses that are sent to the brain. Loud sounds destroy these tiny hair cells in the inner ear. Once about 25% of these cells disappear, you begin to experience hearing loss.
Hearing damage can occur in two ways:
-
Brief exposure to extremely loud sounds can cause permanent damage.
-
Consistent exposure to moderate-level loud sounds wears out the hair cells in the inner ear. Over time, permanent hearing loss occurs as these cells die.
Here is some data from an Internet search on safe use of iPods. Note: The abbreviation dB means decibel—a measure of the loudness of sound.
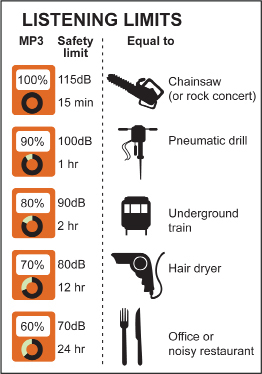
|
Percent of |
Maximum Listening Time per Day |
|||
|
Earbud |
Isolator |
Supra-Aural |
iPod Stock Earphones |
|
|
10–50% |
no limit |
no limit |
no limit |
no limit |
|
60% |
no limit |
14 hours |
no limit |
18 hours |
|
70% |
6 hours |
3.4 hours |
20 hours |
4.6 hours |
|
80% |
1.5 hours |
50 minutes |
4.9 hours |
1.2 hours |
|
90% |
22 minutes |
12 minutes |
1.2 hours |
18 minutes |
|
100% |
5 minutes |
3 minutes |
18 minutes |
5 minutes |
|
Maximum listening time per day using NIOSH damage-risk criteria. “Earbud” includes stock earphones and iPod in-ear earphones. “Isolator” includes Etymotic ER6i earphones and Shure E4c earphones. “Supra-Aural” includes Koss headphones that rest on top of the ear. |
||||
© 2010 Cory D.F. Portnuff, Au.D. and Brian J. Fligor, Sc.D.
Your task is to analyze the data shown in the charts, answer the following questions, and provide a recommendation for safe use of personal music players as supported by mathematical evidence including your choice of equations, graphs, and data tables.
-
Is there a linear relationship between listening time and decibels? Explain how you know.
-
Is there a linear relationship between volume control and decibels? Explain how you know.
-
Is there a linear relationship between listening time and volume control? Explain how you know.
-
Would any graphs you create be continuous or discrete? Explain.
-
Can you figure out the domain and range here? Are there limits for this data?
-
What would be an appropriate independent variable? Explain.
-
Consider the sources of the data and your analysis. Make recommendations for safe use of personal music players.
Save your research and conclusions in your course folder. Your teacher may ask to check your work.
Module 6: Linear Equations
Lesson 4 Summary
In this lesson you investigated the following questions:
-
How are the fixed and variable elements of a problem related to the linear equation y = mx + b?
-
How do you apply techniques and concepts learned in this module to solve problems?
In this final lesson of Module 6 you tackled applications of linear relations. You used what you learned in the previous lessons of this module to solve linear problems. You interpreted linear functions expressed in function notation. You learned that a linear equation has a fixed term and a variable term corresponding to the mx-term and the b-term, respectively, in the equation y = mx + b. The fixed and variable terms can be used to translate descriptions of linear relations into equations. You worked through interactive lessons, studied examples, and tried different exercises to practise constructing and using equations to model linear situations.
In the Math Lab you gathered data by counting the beats to a favourite song. You then constructed an equation to model the linear relation between beats and elapsed time. Through this activity you may have learned to appreciate a systematic approach to mathematical problem solving. This approach involves breaking the solution into smaller parts including the following:
-
identify and assign variables
-
sketch a graph
-
construct an equation
-
use the equation to predict other values
Strategies may differ slightly but each component listed above is essential to a complete solution.
In the next module you will consider systems of two linear equations. You will solve systems of equations in various ways, from graphical methods to algebraic methods. Your mastery of the concepts in this module will serve as a strong foundation as you move into the remaining lessons in this course.