Print bookPrint book

Lesson 1

Site: MoodleHUB.ca 🍁
Course: Math 20-2 SS
Book: Lesson 1
Printed by: Guest user
Date: Saturday, 6 September 2025, 2:32 AM

Description

Created by IMSreader

Table of contents

1. Lesson 1

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 

Lesson 1: Working with Multiple Triangles

 
Focus
 

Trigonometry can be used to determine distances and angles when it is not feasible to measure them directly.

 

For example, Gerard is a window washer who charges his clients based on the area to be washed. He knows the width of an office tower, but he also needs the height. Although he dressed up as Spiderman at Halloween, he can’t crawl up the outside of buildings. This means that he can’t just use a tape measure to determine the building’s height. He could, however, stand on the roof of an adjacent building and determine the height indirectly using trigonometry.

 

angle of depression: an angle with one horizontal arm, and one arm below horizontal

 

angle of elevation:an angle with one horizontal arm and one arm above horizontal

From the top of the adjacent building, Gerard uses a clinometer and determines that the angle of depression to the base of the office tower is 38° and the angle of elevation to the top of the office tower is 52°.



glossary

You will be presented with a number of definitions in this lesson. Remember to add any definitions and corresponding diagrams to your Glossary Terms document.

Gerard’s first step would be to draw a diagram. He might draw one like this:

 

 

This is a picture of two adjacent office buildings. The angle of depression from the top of the shorter building to the bottom of the taller building is 38 degrees. The angle of elevation from the top of the shorter building to the top of the taller building is 52 degrees.

 

You will notice that the diagram Gerard drew has two right triangles. You might remember from previous math courses that knowledge of trigonometry and the Pythagorean theorem will be helpful in solving problems that involve triangles.

 

In this lesson you will use the primary trigonometric ratios and the Pythagorean theorem to solve problems involving multiple right triangles.

 

This lesson will help you answer the following inquiry question:

  • How can you use multiple triangles to solve indirect measurement problems?

    Important!

     

    Your calculator must be set to degree mode for all calculations done in Mathematics 20-2.

     

    Just like there are different units of measure for distance (e.g., kilometres and centimetres), there are different units of measure for angles (e.g., degrees and radians). And just like you would get an incorrect answer if you used kilometres where centimetres were expected, you will get incorrect answers if you use radians or grads instead of degrees.

     

    Have a look at your calculator screen. Typical calculators will show “Deg,” “Rad,” or “Grad.” If your calculator shows “Deg,” it is in degree mode. If your calculator shows either “Rad” or “Grad,” you need to press the Mode or DRG button until you see “Deg.”

     

    If you cannot determine how to set your calculator to degree mode, you will need your calculator’s manual. These manuals can often be found on the Internet by entering your calculator’s make and model number into a search engine.



Assessment

This lesson provides you with opportunities to investigate, discuss, and practise the knowledge and skills you are learning. For instance, in Try This and Share, you can check your answers with other students to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.

 

All assessment items you encounter need to be placed in your course folder. You should have already had a discussion with your teacher about which items you will be handing in for marking. Make sure you follow your teacher’s instructions.

 

course folder

Save a copy of the Lesson 1 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.


 

Time

 

Each module is made up of lessons. Each lesson in Mathematics 20-2 is designed to be completed in approximately 80 minutes. You may find that you require more or less time to complete different lessons depending on your strengths. It is important that you progress at your own pace based on your individual learning requirements.

an instrument that can be used to measure the angle between a horizontal line and the line of sight to another object


1.1. Launch

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Launch
 

In a previous math course, you learned the primary trigonometric ratios:

You also learned the Pythagorean theorem:

 

 

a2 + b2 = c2


formula
Recall from the Course Introduction that you will be creating a formula sheet in this course. Now is a good time to add any formulas to the Formula Sheet document. You should save your Formula Sheet document to your course folder.

You may remember these ratios with the acronym SOH CAH TOA. The SOH CAH TOA Animation should help you remember these ratios.

 

 

This is a screenshot for SOH CAH TOA Animation.

Before working with multiple triangle problems, you should ensure you are comfortable with the primary trigonometric ratios and the Pythagorean theorem.


 

1.2. Are You Ready?

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Are You Ready?

 

This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully. Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.

  1. Find the unknown length. State your answers rounded to the nearest tenth.


    1. This is a picture of a right triangle with a 27 degree angle. The side opposite the 27 degree angle is labelled x, and the length of the hypotenuse is 25 m.

      Answer


    2. This is a picture of a right triangle with a 63 degree angle. The side opposite the 63 degree angle is 15 m, and the side adjacent to the 63 degree angle is labelled x.

      Answer


    3. This is a picture of a right triangle with a 48 degree angle. The side adjacent to the 48 degree angle is 8 m, and the hypotenuse is labelled y.

      Answer


    4. This is a picture of a right triangle. The hypotenuse is 9.2 m, one of the other two sides is labelled a, and the last side is 7 m.

      Answer

  2. Find the unknown angle. State your answers rounded to the newest whole number.


    1. This is a picture of a right triangle with one of the non-90 degree angles labelled theta. The side adjacent to theta is 4 cm, and the hypotenuse is 5 cm.

      Answer


    2. This is a picture of a right triangle with one of the non-90 degree angles labelled theta. The side opposite to theta is 4.3 cm, and the hypotenuse is 5.2 cm.

      Answer

 

1.3. Refresher

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Refresher
 

This section will help refresh your memory on the use of primary trigonometric ratios and the Pythagorean theorem. Look at this section if you had difficulty with the questions from Are You Ready?

 

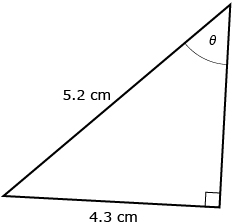
You may find it helpful to review Three Sides of a Right Triangle from the Mathematics 10C course.

 

 

This play button opens up Three Sides of a Right Triangle.

 

The definitions for the primary trigonometric ratios are given in the following table.

 

Trigonometric Ratio Definition Formula
sine the ratio of the length of the side opposite the reference angle to the length of the hypotenuse
cosine the ratio of the length of the side adjacent to the reference angle to the length of the hypotenuse
tangent the ratio of the length of the side opposite the reference angle to the length of the side adjacent to the reference angle


The interactive piece titled “Exploring Trigonometry” allows you to practise identifying the sides of a triangle by dragging and dropping the opposite, adjacent, and hypotenuse sides into their correct locations. You can find the interactive piece on the right-hand side of the website.

 

 

This is a screenshot for Exploring Trigonometry.

 

The sine, cosine, and tangent ratios can be used to determine lengths of sides and measures of angles. When you open the piece titled Finding Angles and Lengths Using Sine, Cosine, and Tangent Ratios, you can view examples of how each ratio is used.

 

 

This is a screenshot for Finding Angles and Lengths Using Sine, Cosine, and Tangent Ratios.

 

Under the Finding Angles box, click “Sine,” “Cosine,” and “Tangent” to see examples of how each ratio can be used to determine missing angles depending on the information that you have. Then, under the Finding Lengths box, click “Sine,” “Cosine,” and “Tangent” to see examples of how each ratio can help to find missing side lengths in a right triangle.

You should now be more comfortable using the primary trigonometric ratios.

 

The Pythagorean theorem is defined as a2 + b2 = c2 where a and b are sides adjacent to the right angle and c is the longest side, called the hypotenuse.

 

Example 1

 

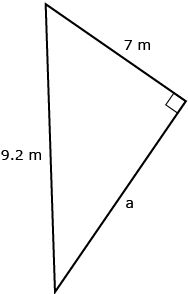
Find y. The answer should be rounded to the nearest tenth of a metre.

 

 

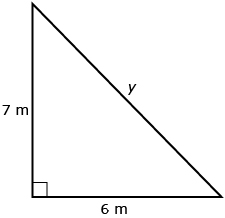
This is a picture of a right triangle. The hypotenuse is labelled y, and the other two sides are 6 m and 7 m.

 

Use the Pythagorean theorem.

 

 

 

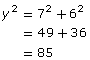
Take the square root of both sides.

 

 

y = 9.2 m

 

Example 2

 

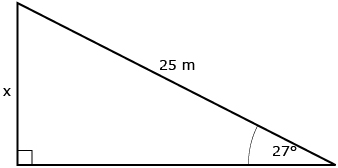
Determine x.

 

 

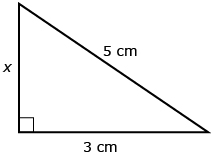
This is a picture of a right triangle. The hypotenuse is 5 cm, one side is 3 cm, and the last side is labelled x.

 

Use the Pythagorean theorem.

 

 

 

Go back to the section titled Are You Ready? Try the questions again. If you are still having difficulty, contact your teacher.


 

1.4. Discover

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Discover
 

In previous math courses, the emphasis in trigonometry was single triangle problems. In Mathematics 20-2 you will be solving a variety of problems involving more than one triangle. In this section you will examine problems that involve more than one triangle and the strategies for solving for sides and angles.

 

Share 1

 

course folder

After a discussion with your teacher, you will decide how to connect with other students for Share activities. Follow your teacher’s instructions to complete this Share activity. Place a summary of your Share discussion in your course folder. For more information on Share discussions, refer to the Course Introduction.

 

Eamon was asked to determine the length of side w in the following diagram.

 

 

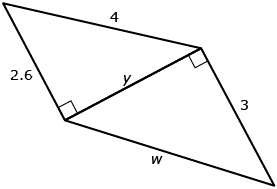
This is a picture of two right triangles that share a side labelled y. The first triangle has a hypotenuse with length 4 units. One side is labelled y, and the final side has a length of 2.6 units. The second triangle has a hypotenuse labelled w, one side has a length of 3 units, and the final side is labelled y.

 

Eamon used the following steps to determine the length of side w:

 

Step 1: y2 + 2.62 = 42

 

Step 2: y2 + 6.76 = 16

 

Step 3: y2 = 16 − 6.76

 

Step 4: y2 = 9.24

 

Step 5:

 

Step 6: y = 3.0397...

 

Step 7: y = 3.0

Step 8: 32 + y2 = w2

 

Step 9: 9 + 9.24 = w2

 

Step 10: 18.24 = w2

 

Step 11:

 

Step 12: w = 4.2708...

 

Step 13: w = 4.3

 

 

 

With a partner, discuss and come to agreement on the following questions.

  1. The set of steps have been split into two groups. Describe what Eamon was doing in the left column, and describe what he was doing in the right column.

  2. Why did Eamon perform the steps in the left column?
Share 2
 

Nasreen was asked to determine the length of side p in the following diagram.

 

 

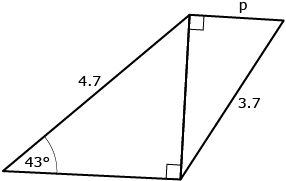
This is a picture of two right triangles that share an unlabelled side. The first triangle has a 43 degree angle. The hypotenuse has a length of 4.7 units, the side adjacent to the 43 degree angle is unlabelled, and the side opposite to the 43 degree angle (unlabelled) is shared with the second triangle. The second triangle has a hypotenuse with length 3.7 units. The side not shared with the first triangle is labelled p.

 

Nasreen used the following steps to determine the length of side p:

 

Step 1:

 

Step 2:

 

Step 3: 4.7(sin 43°) = y

 

Step 4: y = 2.6282...

 

Step 5: y = 2.6

 

Step 6: p2 + y2 = 3.72

Step 7: p2 + (2.6282...)2 = 3.72

 

Step 8: p2 − 13.69 − (2.6282...)2

 

Step 9: p2 = 10.4846...

 

Step 10:

 

Step 11: p = 3.2379...

 

Step 12: p = 3.2

 

 


Notice that Nasreen did not round her answers until she got to the final answer of the problem.

 

With a partner, discuss and come to agreement on the following questions.

  1. The set of steps have been split into two groups. Describe what Nasreen was doing in the left column, and describe what she was doing in the right column.

  2. Why did Nasreen perform the steps in the left column?

  3. Nasreen and Eamon both chose to group their solutions into two sets of steps. What is similar about their groupings?

 

1.5. Explore

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Explore

 

Problems involving more than one triangle that share sides are very common. Using shared sides in triangles is, in fact, the core of triangulation used in map-making. If there is not enough information in a triangle to solve it, then a second triangle that shares one side is often used. Consider the following example.

 

Giovanni and Nakato work for a surveying company and they have been asked to survey the route for a new road. They need to determine the distance from point A to point D where the road will be constructed (marked as b on the following diagram). Unfortunately, this route goes through the middle of some marshland that is very wet, and they cannot directly measure between points A and D. Giovanni measured the distance between points C to B and ∠C and ∠ABD.

 

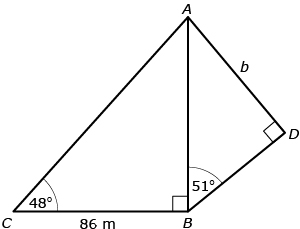
This is a picture of two right triangles: triangle ABC and ABD share side AB. In triangle ABC, side AC is the hypotenuse whose length is unknown, side CB has a length of 86 m, and side AB (shared with the second triangle) has an unknown length. Angle B equals 90 degrees and angle C equals 48 degrees. In triangle ABD, side AB is the hypotenuse whose length is unknown, and side AD is labelled b. Angle D equals 90 degrees and angle B equals 51 degrees.

 

Giovanni has created a problem where two triangles share a side. can be used as a first step in solving for side b in . Nakato decided to solve for the length of side AB and then used that to solve for the length of side b. Here is her solution for the length of AB:

 

Nakato chooses to use the tangent ratio.
Multiply both sides by 86 as a first step in isolating AB.
86(tan 48°) = AB

The number 86 is cancelled on the right side.

AB = 95.5126...

 Nakato has not rounded this number because it is not the final answer to this problem.

 

Nakato continues, being sure to use her unrounded answer for the length of AB. The following is Nakato’s solution for the length of side b.

 

Nakato is writing AB instead of 95.5126... so she remembers to use the unrounded length of AB (see below).
Multiply both sides by AB in order to isolate b.
AB(sin 51°) = b AB is cancelled on the right side.
(95.5126...) (sin 51°) = b

Now Nakato replaces AB with the unrounded value calculated above.

 

tip

Calculators often have an ANS key to signify the last calculated number. In this case, Nakato could enter ANS (sin 51°) in her calculator.

 
b = 74.2272...

The unrounded value of b is 74.2272...
b = 74.2 m Unless stated otherwise, round distances to the nearest tenth.


Although these examples have concentrated on problems involving triangulation, multiple triangle problems show up in other areas where distances cannot be measured directly. You will work with some of these areas in the following Self-Check.


 

1.6. Explore 2

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Self-Check 1

 

Be sure to check your answers to ensure that you understand the solution process.

  1. Now that you have looked at a number of examples involving two right triangles, Gerard’s problem from the beginning of this lesson can be solved. Recall that he wants to determine the height of an office building. Using the two triangles Gerard drew, calculate the height of the office building.

    To view the solution, watch Gerard’s Solution.

     
    This is a screenshot for Gerard’s Solution.

textbook
  1. Complete “Practising” question 5 on page 161 of your textbook. Answer

  2. Complete “Practising” question 10 on page 168 of your textbook. Answer

notes organizer
In this lesson you learned about applying the Pythagorean theorem and the primary trigonometric ratios (SOH CAH TOA) to solve problems involving multiple triangles. If you haven’t done so already, update your notes organizer with any thoughts or key ideas about these types of problems. For instance, you might find it helpful to write down how SOH CAH TOA can help you remember the primary trigonometric ratios.

 

1.7. Connect

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Connect
 
Lesson Assignment


assessment

Go to the Lesson 1 Assignment that you saved to your course folder. Complete the questions.

 

As you complete this assignment, you may wish to answer electronically. To learn how to insert equations into a Word document, such as your lesson assignment, watch the video Inserting Equations in MS Word 2007. The video Inserting Shapes in MS Word 2007 shows how to insert shapes into a Word document.

 

 

This is a screenshot for Inserting Equations in MS Word 2007.

 

 

This is a screenshot for Inserting Shapes in MS Word 2007.


 

1.8. Lesson 1 Summary

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Lesson 1 Summary

 

When determining distances or angles in real-world problems, you often end up with diagrams that contain two right triangles that share a side. You can often use the primary trigonometric ratios to solve for the shared side in the first triangle; then use that side length to solve for a side or angle in the second triangle.

 

Remember that “primary trigonometric ratios” is the fancy way of referring to the following equations:

In the next lesson you will learn about trigonometry for oblique triangles (i.e., triangles that do not contain a 90° angle).