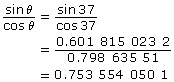Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 5:25 AM |
Description
Created by IMSreader
1. Lesson 2
Module 1: Trigonometry
Lesson 2: The Sine Law
Focus

iStockphoto/Thinkstock
Did you notice that in the previous lesson you were only working with right triangles? Not all problems involve right triangles. For instance, the original maps of Britain were based on survey work done between 1783 and 1853. In the early twentieth century, the British government realized that their maps were not completely accurate and decided to create new maps for all of Britain. The triangulation method of surveying was used to complete the Retriangulation of Britain (1935–1962). Concrete pillars called trig points were created all around the country. These pillars became the vertices of triangles that were used to create accurate maps of Britain. Trigonometry played an important role in helping to calculate the angles and distances between trig points.
Trig point locations were chosen for maximum visibility—the British didn’t have the luxury of creating right triangles. As a result, math that is valid for all triangles, including oblique triangles, was used.
![]()
Remember that an oblique triangle is a triangle that does not have a 90° angle.
Today, if you were to use triangulation to measure distances around Lesser Slave Lake, you might end up with trig points and corresponding triangles at these locations:
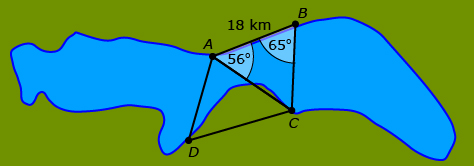
There are no right triangles in this diagram, only oblique triangles. You need to be certain that the method for solving this problem is valid for oblique triangles.
This lesson will help you answer the following inquiry questions:
- Do the Pythagorean theorem and the primary trigonometric ratios (sine, cosine, and tangent) work when solving oblique triangle problems?
- What formulas can be used to solve for angles and sides in any triangle (including oblique triangles)?
Assessment
- Lesson 2 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 2 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.1. Discover
Module 1: Trigonometry
Discover
In Lesson 1 you used the Pythagorean theorem and the primary trigonometric ratios to solve problems involving triangles. Since you only used these formulas for right triangles, you should investigate if they are valid for oblique triangles.
Try This 1
You should place your completed Try This activities in your course folder. Your teacher may ask to see your completed Try This activities.
Use the Pythagorean Theorem Explorer applet to investigate the types of triangles where a2 + b2 = c2 is valid and where it is not valid. As you drag the points, you will see how the different pieces of the Pythagorean theorem relate to each other.
Think about the following questions while you use the Pythagorean Theorem Explorer:
- What types of triangles make a2 + b2 = c2?
- What types of triangles make a2 + b2 ≠ c2?
- What do a, b, and c in the Pythagorean theorem represent?
Share 1
Compare your conclusions with a partner. With your partner, answer the following questions:
- What types of triangles make a2 + b2 = c2?
- What types of triangles make a2 + b2 ≠ c2?
- The letters in the Pythagorean theorem represent specific sides in a triangle. Which one side (a, b, or c) gives you a hint that the formula may not be valid for all triangles? Explain why.
![]() Place a copy of your conclusions in your course folder.
Place a copy of your conclusions in your course folder.
1.2. Discover 2
Module 1: Trigonometry
In the previous activity you saw that the Pythagorean theorem is only valid for right triangles. What about the primary trigonometric ratios—can they be used to solve for missing measurements in oblique triangles? A close examination of these ratios will answer this question.
The sine and cosine ratios require the length of the hypotenuse. Since the hypotenuse is defined to be the side across from a right angle, you can only talk about hypotenuse if you have a right triangle. For this reason, the sine and cosine ratios only make sense for a right triangle.
Another way to define the tangent ratio is using the sine and cosine ratios.
![]()
You can check this using any acute angle. Try 37° and put each side of the equation into a table.
|
|
|
Since the tangent ratio can be written as the quotient of the sine and cosine ratios, the tangent ratio will also only work for right triangles.
1.3. Discover 3
Module 1: Trigonometry
The primary trigonometric ratios are only valid for right triangles, so how are problems involving oblique triangles solved? The following tool will help you discover a formula that is true for all triangles, including oblique triangles.
Try This 2
The Sine Law Explorer applet compares the ratios of sides and sines of angles. Drag the points of the triangle to change the measure of the angles and lengths of sides. Observe what happens to the ratios.
Share 2
Compare your observations from Try This 2 with a partner. With your partner, describe an equation or relationship that appears to be true for all triangles.
![]() Place a copy of your conclusion in your course folder.
Place a copy of your conclusion in your course folder.
1.4. Explore
Module 1: Trigonometry
Explore
The relationship you discovered above in the Try This 2 and Share 2 activities is called the sine law and is valid for all triangles, including both right triangles and oblique triangles. It is usually written in the following way:
![]()
This is a short-hand way of writing three separate equations:
This mathematical expression could be written in words as “The length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle.” The animation Sine Law Illustrator shows this pictorially.
This formula reflects how mathematicians typically label triangles: sides are named with lowercase letters and angles are named with uppercase letters. Sides and their opposite angles are named with the same letter—for example, b and B.
You may find it helpful to view How to Label a Triangle.
You may want to add the sine law to your Formula Sheet document. Remember to save your updated Formula Sheet to your course folder.
1.5. Explore 2
Module 1: Trigonometry
The sine law can be used to solve for side lengths in triangles, such as in the following example.
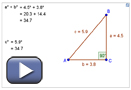
Khadija is building a walkway from her back door to a shed at the back of her yard. She needs to provide the length to a contractor in order to get a phone estimate for the cost. She knows her house is 10.7 m wide and has measured two angles as shown in the following diagram.
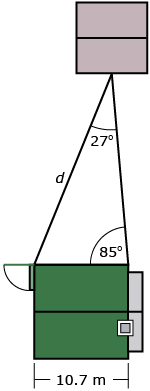
Khadija can use the sine law to determine the distance from her house to the shed (d on the diagram).
|
|
Write the sine law using a side-angle pair that you know and the side-angle pair with your unknown distance. |
|
|
Multiply both sides by sin 85° in order to isolate d. |
|
|
Cancel sin 85° to isolate d. |
|
d = 23.4791… m
|
The unrounded value of d is 23.4791... |
|
d = 23.5 m
|
Unless stated otherwise, distances should be rounded to the nearest tenth. |
Read “Example 1: Using reasoning to determine the length of a side” on page 134 of your textbook. As with the preceding example, Elizabeth is not working with a right triangle, so the primary trigonometric ratios cannot be used. Notice how Elizabeth was careful to pair sides with the angles across from them.
Ensure that you are comfortable with the steps in this solution before moving on.
1.6. Explore 3
Module 1: Trigonometry
Self-Check 1
Complete the following questions. Be sure to check your answers to ensure that you understand the solution process.
1.7. Explore 4
Module 1: Trigonometry
The sine law can also be used to solve for angles. When using the sine law, rearranging the formula is easier when the unknown is in the numerator. The following equivalent form of the sine law is usually used when solving for angles:
![]()
Read “Communication Tip” in the margin of page 136 of your textbook to learn about compass directions.

BananaStock/Thinkstock
Example
Jeremy is learning how to use a compass in an orienteering course. The instructions he was given tell him that he must walk 70 m from Checkpoint A to Checkpoint B. He knows that Checkpoint A is directly north of him and Checkpoint B is in a direction of N41°E. He also knows that Checkpoint B is 105 m from Checkpoint C. He begins by drawing a diagram to represent his situation.
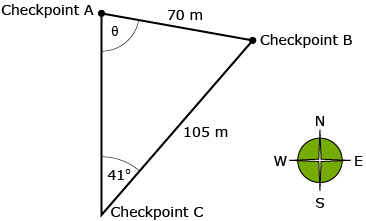
Jeremy needs to determine the direction to walk when going from Checkpoint A to Checkpoint B.
From the diagram he drew, he knows that once he determines angle θ he will be able to state the direction as Sθ°E. Jeremy looks at the given information and recognizes that he can use the sine law to determine this angle. His solution can be seen in the animation Jeremy’s Solution: Example 2.
Read “Example 3: Using reasoning to determine the measure of an angle” on page 136 of your textbook. As with the preceding example, Anthony has been asked to determine a direction. You will learn more about parallel lines and transversals, which are used in the second half of Anthony’s solution in Module 2: Logic and Geometry.
Ensure that you are comfortable with the steps in this solution before moving on.
1.8. Explore 5
Module 1: Trigonometry
Self-Check 2
Complete the following questions. Be sure to check your answers to ensure that you understand the solution process.
- Complete “Check Your Understanding” question 2.b. on page 138 of your textbook. Answer
- Complete “Practising” questions 3.d., 3.e., 4, 7, and 8 on pages 139 and 140 of your textbook. (Note: In question 7, you are asked to solve a triangle. This means that you must give the measures of all three sides and all three angles.) Answer
In the Discover section of this lesson, you used the Sine Law Explorer to see a visual justification of the sine law. A mathematician would say that you used “inductive reasoning” to infer that the sine law is true for all triangles. In order to prove that the sine law is always true, you must use a process called “deductive reasoning.”
Read how Ben used deductive reasoning to prove the sine law in “Investigate the Math” on pages 132 and 133 of your textbook.
Try This 3
You may choose to work on your own or with a partner to improve upon Ben’s proof. Answer questions A to F on the bottom of page 133 of your textbook.
![]() Place a copy of your responses in your course folder.
Place a copy of your responses in your course folder.
1.10. Lesson 2 Summary
Module 1: Trigonometry
Lesson 2 Summary
In this lesson you saw that the Pythagorean theorem and the primary trigonometric ratios are only valid for right triangles. You also learned and applied a new formula, the sine law, that is valid for all triangles, including both right and oblique triangles.
![]()
The sine law can help indirectly calculate angles and distances for a variety of purposes.
In the next lesson you will learn another formula that is valid for all triangles: the cosine law.